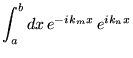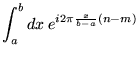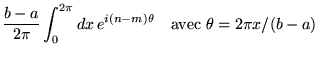suivant: 3.2 Convergence et Complétude
monter: 3 Série de Fourier
précédent: 3 Série de Fourier
Table des matières
On considère l'opérateur linéaire 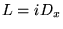 et le produit scalaire sur
l'intervalle
et le produit scalaire sur
l'intervalle ![$ [a,b] $](img203.gif) :
:
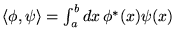 .
Si
.
Si 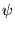 et
et 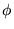 sont des fonctions périodiques (
sont des fonctions périodiques (
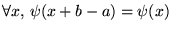 )
montrons que
)
montrons que 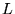 est auto-adjoint par rapport à ce produit scalaire:
est auto-adjoint par rapport à ce produit scalaire:
Les valeurs propres de 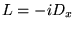 sont donc réelles. De même, pour des
fonctions périodiques,
sont donc réelles. De même, pour des
fonctions périodiques,
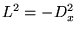 sera auto-adjoint avec des valeurs
propres positives, puisque
sera auto-adjoint avec des valeurs
propres positives, puisque
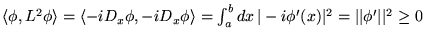 .
.
La fonction propre ou le vecteur propre associé à la valeur
propre réelle 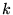 est solution de l'équation différentielle
est solution de l'équation différentielle
solution qui est unique à un facteur multiplicatif près, correspondant à un
sous-espace propre de dimension 1. Pour satisfaire les conditions de périodicité
(C.B.), il faut de plus que
Comme il se doit, les vecteurs propres associés à des valeurs propres distinctes
sont orthogonaux:




suivant: 3.2 Convergence et Complétude
monter: 3 Série de Fourier
précédent: 3 Série de Fourier
Table des matières
2000-10-06
![]() et le produit scalaire sur
l'intervalle
et le produit scalaire sur
l'intervalle ![]() :
:
![]() .
Si
.
Si ![]() et
et ![]() sont des fonctions périodiques (
sont des fonctions périodiques (
![]() )
montrons que
)
montrons que ![]() est auto-adjoint par rapport à ce produit scalaire:
est auto-adjoint par rapport à ce produit scalaire:
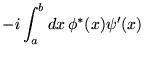
![% latex2html id marker 15785
$\displaystyle -i\left[ \phi ^{*}(x)\psi (x)\right] ^{b}_{a}+i\int ^{b}_{a}dx\, {\phi '}^{*}(x)\psi (x)$](img420.gif)
![]() est solution de l'équation différentielle
est solution de l'équation différentielle
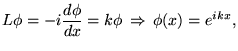
![$\displaystyle \left\{ \begin{array}[t]{l}
k=\frac{2\pi n}{b-a}\doteq k_{n}\\
\phi _{n}=e^{ik_{n}x}
\end{array}\right. \quad \textrm{avec }n=0,\pm 1,\pm 2,\ldots$](img427.gif)