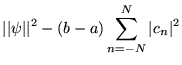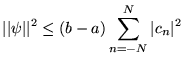


suivant: 3.3 Cas particuliers
monter: 3 Série de Fourier
précédent: 3.1 Fonctions propres de
Table des matières
Sous-sections
Par des combinaisons linéaires des vecteurs 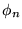 , on génère un espace
vectoriel de dimension infinie, dont chaque vecteur est une fonction, donné
par la série de Fourier
, on génère un espace
vectoriel de dimension infinie, dont chaque vecteur est une fonction, donné
par la série de Fourier
On peut alors se poser deux types de questions:
- comment cette série converge-t-elle, et sous quelles conditions sur les coefficients
de Fourier
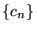 , et
, et
- quel type de fonctions se laissent représenter par une telle série, ou dit autrement,
dans quel espace de fonctions les
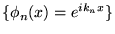 forment-ils
une base.
forment-ils
une base.
Pour utiliser l'image naïve de la section 2.1, les vecteurs
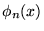 peuvent s'assembler en une matrice de changement de base
peuvent s'assembler en une matrice de changement de base 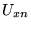 , avec
l'index
, avec
l'index 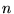 numérotant les vecteurs colonnes et l'index
numérotant les vecteurs colonnes et l'index 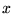 ``numérotant''
les lignes. On peut alors se demander si:
``numérotant''
les lignes. On peut alors se demander si:
-
![% latex2html id marker 15845
$ (U_{xn})^{\dagger }U_{xn'}\begin{array}[b]{c}
?\\
=
\end{array}\mathbb{1}_{nn'} $](img439.gif) qui concerne en fait la convergence de la série de Fourier, et si
qui concerne en fait la convergence de la série de Fourier, et si
-
![% latex2html id marker 15847
$ U_{xn}(U_{x'n})^{\dagger }\begin{array}[b]{c}
?\\
=
\end{array}\mathbb{1}_{xx'} $](img440.gif) qui détermine la complétude de l'ensemble de vecteurs choisis.
qui détermine la complétude de l'ensemble de vecteurs choisis.
La question est la suivante. Partant des coefficients 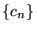 on peut
construire la série de Fourier
on peut
construire la série de Fourier
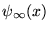 . Dans un espace de
dimension finie, on sait que les produits scalaires
. Dans un espace de
dimension finie, on sait que les produits scalaires
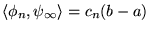 redonnent les coefficients à un coefficient de normalisation près. Ceci n'est
pas garanti en dimension infinie, à moins d'imposer des conditions supplémentaires.
redonnent les coefficients à un coefficient de normalisation près. Ceci n'est
pas garanti en dimension infinie, à moins d'imposer des conditions supplémentaires.
Théorème 3.2
Si les séries partielles
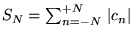
convergent,
alors la série de Fourier converge uniformément vers une fonction
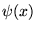
continue
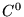
.
Preuve.
En effet, la série partielle
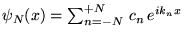
converge
puisque
Puisque
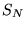
converge,
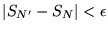
dès que
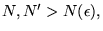
et donc
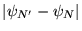
aussi. De plus comme
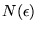
est le même pour chaque
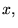
on a convergence uniforme, ce qui garantit
la continuité de la limite
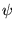
, puisque chaque
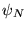
est
continue.

Gràce à la convergence uniforme, on peut intégrer terme à terme, et
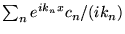 convergera uniformément vers une primitive de
convergera uniformément vers une primitive de 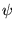 , primitive qui est
donc au moins
, primitive qui est
donc au moins 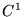 . On peut de même dériver terme à terme, pour autant
que les coefficients de la dérivée
. On peut de même dériver terme à terme, pour autant
que les coefficients de la dérivée
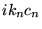 forment une série absolument
convergente. Puisque la convergence des
forment une série absolument
convergente. Puisque la convergence des 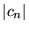 dépend de leur comportement
à grand
dépend de leur comportement
à grand 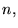 on voit que
on voit que
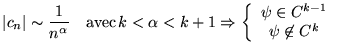 |
(3.2.1) |
En effet, pour 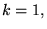 on retrouve que
on retrouve que 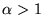 est nécessaire à
la convergence absolue des
est nécessaire à
la convergence absolue des 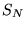 , et donc à la continuité de
, et donc à la continuité de 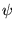 .
Si
.
Si
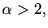 on peut faire le même raisonnement pour la dérivée
on peut faire le même raisonnement pour la dérivée 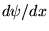 ,
ce qui permet de généraliser à tout entier
,
ce qui permet de généraliser à tout entier 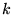 .
.
Théorème 3.2
Si
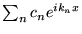
converge uniformément vers
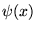
,
alors
Preuve.
En toute rigueur, on a besoin de la convergence uniforme pour intégrer la série
infinie terme à terme et retrouver ce résultat intuitif bien connu dans un espace
de dimension finie. On peut alors être assuré que partant des coefficients
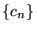
,
si on construit la série Fourier, on obtient une fonction
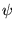
dont
les produits scalaires avec les fonctions
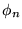
vont bien redonner
les coefficients dont on était parti.

En pratique, c'est la question inverse qui est la plus intéressante: partant
d'une fonction arbitraire 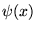 , on peut bien calculer des coefficients
de Fourier
, on peut bien calculer des coefficients
de Fourier
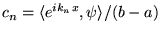 , mais on est
pas assuré que la série de Fourier
, mais on est
pas assuré que la série de Fourier
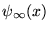 calculée avec ces
coefficients particuliers converge et redonne bien la fonction de départ
calculée avec ces
coefficients particuliers converge et redonne bien la fonction de départ 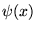 .
Si c'est le cas, les fonctions
.
Si c'est le cas, les fonctions
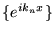 foment un ensemble
complet. Dans le cas contraire, il y aura des fonctions
foment un ensemble
complet. Dans le cas contraire, il y aura des fonctions 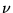 orthogonales
à tous les vecteurs
orthogonales
à tous les vecteurs 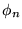 . L'existence de telles fonctions ne fait
aucun doute. On peut par exemple prendre une fonction nulle sur tout le segment
. L'existence de telles fonctions ne fait
aucun doute. On peut par exemple prendre une fonction nulle sur tout le segment
![$ [a,b] $](img203.gif) sauf en un point. Une telle fonction aura un produit scalaire nul
avec tous les
sauf en un point. Une telle fonction aura un produit scalaire nul
avec tous les 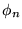 , ainsi d'ailleurs qu'avec n'importe quelle fonction
continue. La question est plutôt de savoir si il est important de pouvoir distinguer
ces fonctions
, ainsi d'ailleurs qu'avec n'importe quelle fonction
continue. La question est plutôt de savoir si il est important de pouvoir distinguer
ces fonctions 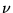 de la fonction nulle. Dans l'exemple donné plus haut
d'une fonction nulle presque partout, la réponse physique est non. On peut aussi
chercher des conditions comme la continuité qui restreignent l'espace de fonctions
considéré, et éliminent ces vecteurs
de la fonction nulle. Dans l'exemple donné plus haut
d'une fonction nulle presque partout, la réponse physique est non. On peut aussi
chercher des conditions comme la continuité qui restreignent l'espace de fonctions
considéré, et éliminent ces vecteurs 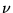 . En réalité, la continuité
est un peu trop forte, on peut se contenter de la continuité par morceaux,
c'est-à-dire la continuité partout sauf en un nombre fini de points.
. En réalité, la continuité
est un peu trop forte, on peut se contenter de la continuité par morceaux,
c'est-à-dire la continuité partout sauf en un nombre fini de points.
Théorème 3.2
Si
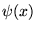
est continue par morceaux sur l'intervalle
![$ [a,b] $](img203.gif)
et
possède partout une dérivée à gauche et une dérivée à droite (éventuellement
différentes), alors la série de Fourier construite avec les
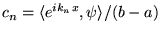
sera
On peut sans changer les 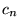 décider qu'aux éventuels points de discontinuité,
décider qu'aux éventuels points de discontinuité,
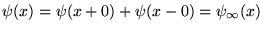 , auquel cas on a un
premier espace vectoriel de fonctions (plus grand que les fonctions
, auquel cas on a un
premier espace vectoriel de fonctions (plus grand que les fonctions 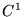 )
dans lequel la base de Fourier est complète. Le fait que ce soit la moyenne
de la valeur à gauche et à droite de
)
dans lequel la base de Fourier est complète. Le fait que ce soit la moyenne
de la valeur à gauche et à droite de 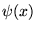 qui intervienne s'appelle
``phénomène de Gibbs''. L'apparition d'une discontinuité dans
qui intervienne s'appelle
``phénomène de Gibbs''. L'apparition d'une discontinuité dans
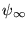 signale l'absence de C.U. de la série de Fourier. Si l'on veut cette convergence,
il faut demander plus:
signale l'absence de C.U. de la série de Fourier. Si l'on veut cette convergence,
il faut demander plus:
Théorème 3.2
Si
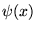
est
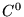
, et
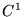
par morceaux, alors sa série
de Fourier converge uniformément vers
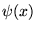
.
Que peut-on dire sans continuité? On admettra sans démonstration.
Théorème 3.2
Si
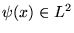
est de carré sommable, alors ses coefficients de
Fourier sont finis et on a l'
égalité de Parseval:
Cette égalité est importante car elle assure que la série partielle de Fourier
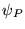 converge en norme
vers
converge en norme
vers 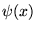 . En effet:
. En effet:
converge bien vers 0 en vertu de l'égalité de Parseval. Tant que 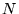 reste
fini, il manque des vecteurs de base, et on a l'inégalité de Bessel:
reste
fini, il manque des vecteurs de base, et on a l'inégalité de Bessel:
La démonstration de l'égalité de Parseval sort du cadre de ce cours, mais il
faut bien réaliser que même en acceptant ce résultat, on n'a pas montré que
toute fonction de 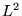 possédait un développement de Fourier unique.
La convergence en norme implique simplement que la différence entre deux fonctions
possédant le même développement est une fonction de norme nulle
possédait un développement de Fourier unique.
La convergence en norme implique simplement que la différence entre deux fonctions
possédant le même développement est une fonction de norme nulle
 L'existence de telles fonctions
L'existence de telles fonctions 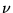 nulles non pas partout, mais seulement
presque partout, montre que la norme quadratique ne satisfait pas aux conditions
de définition d'une bonne norme sur les fonctions. Pour remédier à ce problème,
on pourrait abandonner la norme quadratique au profit de la norme de la convergence
uniforme, mais celle-ci ne dérive pas d'un produit scalaire, ce qui limite grandement
ses possibilités. C'est pourquoi on préfère conserver cette norme, mais travailler
dans un nouvel espace vectoriel
nulles non pas partout, mais seulement
presque partout, montre que la norme quadratique ne satisfait pas aux conditions
de définition d'une bonne norme sur les fonctions. Pour remédier à ce problème,
on pourrait abandonner la norme quadratique au profit de la norme de la convergence
uniforme, mais celle-ci ne dérive pas d'un produit scalaire, ce qui limite grandement
ses possibilités. C'est pourquoi on préfère conserver cette norme, mais travailler
dans un nouvel espace vectoriel
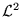 dont chaque point représente
un ensemble de fonctions ne différant que par des fonctions
dont chaque point représente
un ensemble de fonctions ne différant que par des fonctions 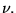 Comme
déjà mentionné dans la section 2.3, les ambiguïtés apportées par
cette imprécision sont sans conséquences en physique où la nature continue de
l'espace-temps n'est jamais qu'une idéalisation invérifiable. Expérimentalement,
les appareils actuels ne peuvent sonder cette continuité que sur des longueurs
supérieures à
Comme
déjà mentionné dans la section 2.3, les ambiguïtés apportées par
cette imprécision sont sans conséquences en physique où la nature continue de
l'espace-temps n'est jamais qu'une idéalisation invérifiable. Expérimentalement,
les appareils actuels ne peuvent sonder cette continuité que sur des longueurs
supérieures à 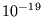 mètre. Du point de vue théorique, pour envisager
sonder des distances inférieures à
mètre. Du point de vue théorique, pour envisager
sonder des distances inférieures à 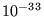 mètres, il faut d'abord réconcilier
la mécanique quantique avec la relativité générale, entreprise si délicate qu'elle
a induit Einstein à se détacher de la mécanique quantique dont il fut pourtant
un fondateur.
mètres, il faut d'abord réconcilier
la mécanique quantique avec la relativité générale, entreprise si délicate qu'elle
a induit Einstein à se détacher de la mécanique quantique dont il fut pourtant
un fondateur.



suivant: 3.3 Cas particuliers
monter: 3 Série de Fourier
précédent: 3.1 Fonctions propres de
Table des matières
2000-10-06
![]() , on génère un espace
vectoriel de dimension infinie, dont chaque vecteur est une fonction, donné
par la série de Fourier
, on génère un espace
vectoriel de dimension infinie, dont chaque vecteur est une fonction, donné
par la série de Fourier
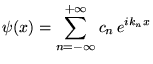
![% latex2html id marker 15845
$ (U_{xn})^{\dagger }U_{xn'}\begin{array}[b]{c}
?\\
=
\end{array}\mathbb{1}_{nn'} $](img439.gif) qui concerne en fait la convergence de la série de Fourier, et si
qui concerne en fait la convergence de la série de Fourier, et si
![% latex2html id marker 15847
$ U_{xn}(U_{x'n})^{\dagger }\begin{array}[b]{c}
?\\
=
\end{array}\mathbb{1}_{xx'} $](img440.gif) qui détermine la complétude de l'ensemble de vecteurs choisis.
qui détermine la complétude de l'ensemble de vecteurs choisis.
![]() on peut
construire la série de Fourier
on peut
construire la série de Fourier
![]() . Dans un espace de
dimension finie, on sait que les produits scalaires
. Dans un espace de
dimension finie, on sait que les produits scalaires
![]() redonnent les coefficients à un coefficient de normalisation près. Ceci n'est
pas garanti en dimension infinie, à moins d'imposer des conditions supplémentaires.
redonnent les coefficients à un coefficient de normalisation près. Ceci n'est
pas garanti en dimension infinie, à moins d'imposer des conditions supplémentaires.
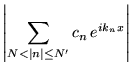
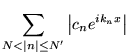
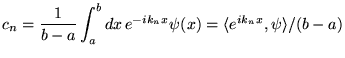
![]() , on peut bien calculer des coefficients
de Fourier
, on peut bien calculer des coefficients
de Fourier
![]() , mais on est
pas assuré que la série de Fourier
, mais on est
pas assuré que la série de Fourier
![]() calculée avec ces
coefficients particuliers converge et redonne bien la fonction de départ
calculée avec ces
coefficients particuliers converge et redonne bien la fonction de départ ![]() .
Si c'est le cas, les fonctions
.
Si c'est le cas, les fonctions
![]() foment un ensemble
complet. Dans le cas contraire, il y aura des fonctions
foment un ensemble
complet. Dans le cas contraire, il y aura des fonctions ![]() orthogonales
à tous les vecteurs
orthogonales
à tous les vecteurs ![]() . L'existence de telles fonctions ne fait
aucun doute. On peut par exemple prendre une fonction nulle sur tout le segment
. L'existence de telles fonctions ne fait
aucun doute. On peut par exemple prendre une fonction nulle sur tout le segment
![]() sauf en un point. Une telle fonction aura un produit scalaire nul
avec tous les
sauf en un point. Une telle fonction aura un produit scalaire nul
avec tous les ![]() , ainsi d'ailleurs qu'avec n'importe quelle fonction
continue. La question est plutôt de savoir si il est important de pouvoir distinguer
ces fonctions
, ainsi d'ailleurs qu'avec n'importe quelle fonction
continue. La question est plutôt de savoir si il est important de pouvoir distinguer
ces fonctions ![]() de la fonction nulle. Dans l'exemple donné plus haut
d'une fonction nulle presque partout, la réponse physique est non. On peut aussi
chercher des conditions comme la continuité qui restreignent l'espace de fonctions
considéré, et éliminent ces vecteurs
de la fonction nulle. Dans l'exemple donné plus haut
d'une fonction nulle presque partout, la réponse physique est non. On peut aussi
chercher des conditions comme la continuité qui restreignent l'espace de fonctions
considéré, et éliminent ces vecteurs ![]() . En réalité, la continuité
est un peu trop forte, on peut se contenter de la continuité par morceaux,
c'est-à-dire la continuité partout sauf en un nombre fini de points.
. En réalité, la continuité
est un peu trop forte, on peut se contenter de la continuité par morceaux,
c'est-à-dire la continuité partout sauf en un nombre fini de points.
![% latex2html id marker 15980
$\displaystyle \psi _{\infty }(x)=\sum ^{+\infty }_{n=-\infty }c_{n}\, e^{ik_{n}x}=\frac{1}{2}\left[ \psi (x+0)+\psi (x-0)\right] $](img474.gif)
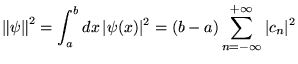
![$\displaystyle \vert\vert\psi \vert\vert^{2}-\sum ^{N}_{n=-N}\left[ c_{n}\langle...
...le +c_{n}^{*}\langle e^{ik_{n}x},\psi \rangle +(b-a)\vert c_{n}\vert^{2}\right]$](img483.gif)