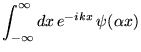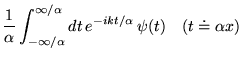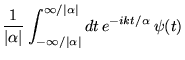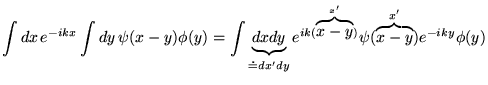


suivant: 4.4 Exemples
monter: 4 Transformée de Fourier
précédent: 4.2 Transformations intégrales
Table des matières
Dans cette section, nous noterons ![$ F[\psi ] $](img553.gif) la transformée de Fourier
la transformée de Fourier
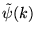 de la fonction
de la fonction 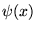 .
.
- Linéarité:
![$ F[\psi +\phi ]=F[\psi ]+F[\phi ] $](img555.gif) .
.
- Si
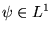 , alors
, alors ![$ F[\psi ] $](img553.gif) est bornée, continue et
s'annule à l'infini:
est bornée, continue et
s'annule à l'infini:
![$ \tilde{\psi }(k)\begin{array}[t]{c}
\rightarrow \\
\vert k\vert\rightarrow \infty
\end{array}0 $](img557.gif) .
.
- Si
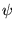 et sa dérivée
et sa dérivée 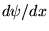 sont sommables (
sont sommables (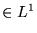 ),
alors on montre (en intégrant par parties) que
Ceci montre que l'opérateur de dérivation
),
alors on montre (en intégrant par parties) que
Ceci montre que l'opérateur de dérivation 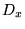 est devenu diagonal après
passage en transformée de Fourier.
est devenu diagonal après
passage en transformée de Fourier.
- Si
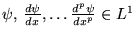 ,
alors pour tout
,
alors pour tout 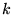 on peut borner
On voit donc que plus
on peut borner
On voit donc que plus 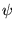 est dérivable, plus vite sa transformée de
Fourier
est dérivable, plus vite sa transformée de
Fourier ![$ F[\psi ] $](img553.gif) décroit à grand
décroit à grand 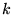 .
.
- Si
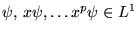 , alors
On voit par là que plus
, alors
On voit par là que plus 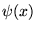 décroit rapidement à l'infini, plus
sa transformée de Fourier
décroit rapidement à l'infini, plus
sa transformée de Fourier ![$ F[\psi ] $](img553.gif) est dérivable.
est dérivable.
- Conjugaison complexe:
ce qui redonne bien
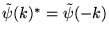 si
si 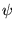 est réelle, comme dans le cas de la série de Fourier.
est réelle, comme dans le cas de la série de Fourier.
- L'opérateur translation est également diagonal en transformée de Fourier, puisque
- Une dilatation
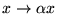 dans l'argument de
dans l'argument de 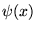 correspond à une contraction en
correspond à une contraction en
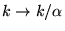 dans l'argument
de sa transformée
dans l'argument
de sa transformée
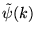 :
Pour bien comprendre ce résultat fondamental, démontrons-le explicitement:
:
Pour bien comprendre ce résultat fondamental, démontrons-le explicitement:
où dans l'avant-dernière ligne, on a renversé l'ordre des bornes d'intégration
si 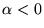 . On voit donc que si la fonction
. On voit donc que si la fonction 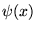 n'est significativement
différente de
n'est significativement
différente de 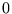 qu'en une région de largeur
qu'en une région de largeur 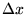 en
en 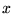 ,
et de même pour sa transformée de Fourier
,
et de même pour sa transformée de Fourier
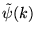 en une région
en une région
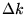 , on doit avoir pour le produit
, on doit avoir pour le produit
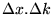 une
constante, indépendante du changement d'échelle
une
constante, indépendante du changement d'échelle 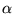 en
en 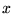 .
Ceci a des répercussions très importantes en théorie du signal. On ne peut par
exemple s'assurer que
.
Ceci a des répercussions très importantes en théorie du signal. On ne peut par
exemple s'assurer que
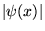 est monochromatique (petit
est monochromatique (petit
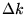 ) que si on la mesure sur un grand domaine
) que si on la mesure sur un grand domaine 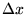 : incertitude
position-vecteur d'onde (ou si on prend
: incertitude
position-vecteur d'onde (ou si on prend 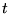 et
et
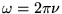 :
incertitude temps-fréquence
:
incertitude temps-fréquence
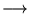 plus une note est grave,
plus il faut la jouer longtemps pour savoir si elle est juste).
plus une note est grave,
plus il faut la jouer longtemps pour savoir si elle est juste).
Pour
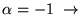 si
si 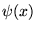 est (im)paire,
est (im)paire,
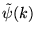 aussi.
aussi.
- Composition:
en effet:



suivant: 4.4 Exemples
monter: 4 Transformée de Fourier
précédent: 4.2 Transformations intégrales
Table des matières
2000-10-06
![]() la transformée de Fourier
la transformée de Fourier
![]() de la fonction
de la fonction ![]() .
.
![$ \tilde{\psi }(k)\begin{array}[t]{c}
\rightarrow \\
\vert k\vert\rightarrow \infty
\end{array}0 $](img557.gif) .
.
![$\displaystyle \vert F[\psi ]\vert=\left\vert \frac{F[d^{p}\psi /dx^{p}]}{k^{p}}\right\vert \leq \frac{C}{k^{p}}.$](img561.gif)
![% latex2html id marker 16300
$\displaystyle \boxed{F[x^{l}\psi ]=i^{l}\frac{d^{l}}{dk^{l}}F[\psi ]};\quad \mathrm{pour}\, l=0\ldots p.$](img563.gif)
=\frac{1}{\vert\alpha \vert}F[\psi (x)](k/\alpha )}$](img569.gif)