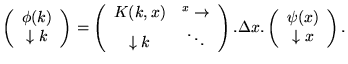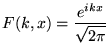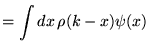4.2 Transformations intégrales

On définit une transformation intégrale de noyau $K(k,x)$ comme l'application linéaire

$$K:\, \psi (x)\rightarrow \phi (k)=K[\psi ](k)=\int dx\, K(k,x)\psi (x)$$

Intuitivement, on peut voir le noyau $K(k,x)$ comme une sorte de matrice:

$$\left( \begin{array}{c} \phi (k)\\ ... ...\Delta x.\left( \begin{array}{c} \psi (x)\\ \downarrow x \end{array}\right) .$$

Exemple 4.2   La transformée de Fourier est une transformation intégrale de noyau

$$F(k,x)=\frac{e^{ikx}}{\sqrt{2\pi }}$$

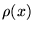
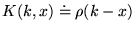
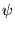
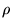
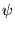
Exemple 4.2   Toute fonction $\rho (x)$ peut donner un noyau intégral par $K(k,x)\doteq \rho (k-x)$. L'image d'une fonction $\psi$ par un tel noyau est par définition le produit de convolution des fonction $\rho$ et $\psi$, et il se note:

$$\phi \doteq \rho \star \psi$$

$$\Leftrightarrow \phi (k) =\int dx\, \rho (k-x)\psi (x)$$

Il faut bien réaliser que l'application définie par un noyau $K$ ne possède pas nécessairement d'inverse. Par exemple, $K(k,x)=k$ est une ``matrice'' non inversible, puisque toutes ses ``lignes'' sont indentiques.