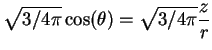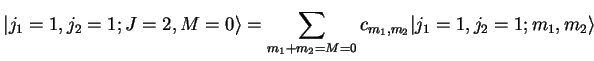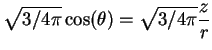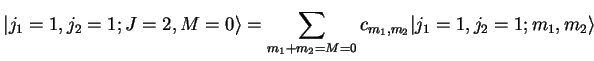

Next: Oscillations dans un système
Up: td00
Previous: td00
- Représentation vectorielle
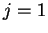 : Calculer les éléments de matrice
de
: Calculer les éléments de matrice
de 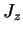 dans la base
dans la base
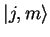 , pour le sous-espace vectoriel
, pour le sous-espace vectoriel
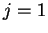 . Les vecteurs
. Les vecteurs
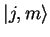 sont par définition orthonormés:
sont par définition orthonormés:
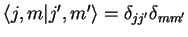 , et on suppose l'état
, et on suppose l'état
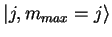 non-dégénéré. Les relations de commutation
non-dégénéré. Les relations de commutation
![$\displaystyle [J_{z},J_{\pm }]=\pm \hbar J_{\pm };\quad [J_{+},J_{-}]=2\hbar J_{z}$](img6.gif) |
(1) |
et l'orthonormalisation permettent-elles de choisir librement la phase des
éléments
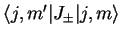 ? Si oui on les prendra positifs: sont-ils
alors complètement déterminés?
? Si oui on les prendra positifs: sont-ils
alors complètement déterminés?
- En déduire les éléments de matrices de
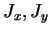 , si
, si
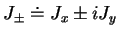 .
.
- On introduit une autre base orthonormée
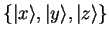 dans le même espace des états à 3 dimensions, avec pour les seuls produits scalaires
non-nuls:
dans le même espace des états à 3 dimensions, avec pour les seuls produits scalaires
non-nuls:
Montrer que les éléments de matrices des 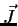 dans cette nouvelle
base redonne (à un facteur
dans cette nouvelle
base redonne (à un facteur 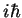 près) les générateurs des rotations:
près) les générateurs des rotations:
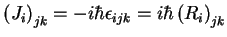 .
Faire le lien avec les harmoniques sphériques:
.
Faire le lien avec les harmoniques sphériques:
- Mesures: Calculer la valeur moyenne et la variance des opérateurs
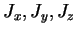 ,
,
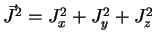 dans chacun des 3 états de
la base
dans chacun des 3 états de
la base
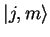 . Quel(s) état(s) minimise(nt) l'incertitude
. Quel(s) état(s) minimise(nt) l'incertitude
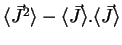 sur le vecteur
sur le vecteur 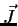 ? Montrer que ces mêmes états saturent la relation
d'incertitude
? Montrer que ces mêmes états saturent la relation
d'incertitude
![$ \Delta J_{x}\Delta J_{y}\geq \vert\langle i[J_{x},J_{y}]\rangle \vert/2 $](img28.gif) .
.
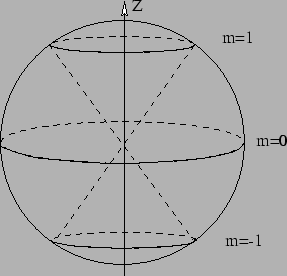
- Image géométrique: On peut tenter de voir le moment angulaire quantique
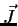 dans ces différents états comme un vecteur de longueur
dans ces différents états comme un vecteur de longueur
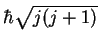 dont la projection sur
dont la projection sur 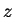 est fixée à
est fixée à 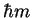 et qui tourne très
rapidement autour de l'axe
et qui tourne très
rapidement autour de l'axe 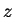 , donnant une moyenne nulle pour
, donnant une moyenne nulle pour 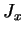 ou
ou 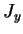 (un peu comme l'image du nuage électronique délocalisé d'un
atome). Cette image permet-elle de comprendre qu'une certaine combinaison linéaire
des états
(un peu comme l'image du nuage électronique délocalisé d'un
atome). Cette image permet-elle de comprendre qu'une certaine combinaison linéaire
des états
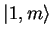 est état propre de
est état propre de 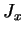 avec la valeur propre
avec la valeur propre
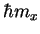 ? Donner cet état pour
? Donner cet état pour 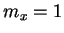 .
.
- Opérateurs vectoriels: le moment cinétique
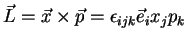 fournit une représentation des ``petites'' rotations sur l'espace vectoriel
des fonctions de
fournit une représentation des ``petites'' rotations sur l'espace vectoriel
des fonctions de 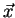 et de
et de 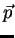 . Montrer en utilisant les
relations de commutations canoniques
. Montrer en utilisant les
relations de commutations canoniques
![$ [x_{i},p_{j}]=i\hbar \delta _{ij} $](img41.gif) que:
que:
- Composition: si
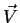 et
et 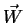 sont 2 opérateurs
vectoriels (c-à-d se transformant sous les rotations comme ci-dessus) qui commutent
entre eux, montrer que
sont 2 opérateurs
vectoriels (c-à-d se transformant sous les rotations comme ci-dessus) qui commutent
entre eux, montrer que
![$ [L_{i},V_{j}W_{k}] $](img47.gif) est une combinaison linéaire
des 9 opérateurs
est une combinaison linéaire
des 9 opérateurs
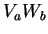 . Montrer que la partie scalaire (1 opérateur
. Montrer que la partie scalaire (1 opérateur
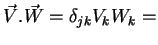 Tr
Tr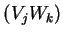 ), antisymétrique
(3 opérateurs
), antisymétrique
(3 opérateurs
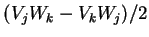 ) et symétrique sans trace (5
opérateurs
) et symétrique sans trace (5
opérateurs
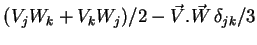 ) ne se mélangent pas entre elles sous les rotations.
) ne se mélangent pas entre elles sous les rotations.
- En particulier, si
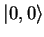 est l'état invariant (c.à-d.
est l'état invariant (c.à-d.
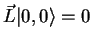 ),
montrer que s'is ne sont pas nuls, les 3 états
),
montrer que s'is ne sont pas nuls, les 3 états
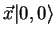 forment
une représentation irréductible de dimension
forment
une représentation irréductible de dimension 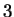 des rotations. Montrer
de même que les 6 états obtenus par l'application des 6 opérateurs
des rotations. Montrer
de même que les 6 états obtenus par l'application des 6 opérateurs
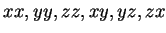 sur l'état invariant forment une représentation réductible en un invariant
sur l'état invariant forment une représentation réductible en un invariant
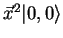 et une représentation de dimension 5. Faire le lien avec les harmoniques sphériques.
Pouvez-vous généraliser et conclure qu'un opérateur vectoriel fait passer d'une
representation
et une représentation de dimension 5. Faire le lien avec les harmoniques sphériques.
Pouvez-vous généraliser et conclure qu'un opérateur vectoriel fait passer d'une
representation 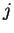 à une représentation
à une représentation 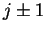 ?
?
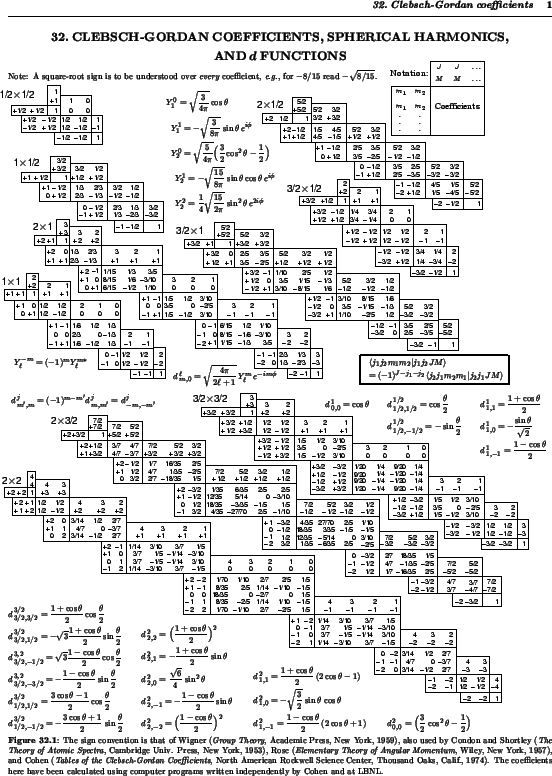
- Clebsch-Gordan: Utilisez la table ci-dessous pour écrire
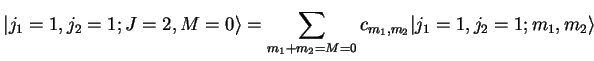 |
(2) |
- [ex. supplém.] Si
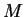 est une matrice
est une matrice 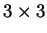 agissant dans
l'espace à 3 dimensions, elle se transforme sous une rotation
agissant dans
l'espace à 3 dimensions, elle se transforme sous une rotation
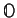 en une nouvelle matrice
en une nouvelle matrice
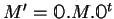 . Montrer que
si on range les 9 éléments de matrices de
. Montrer que
si on range les 9 éléments de matrices de 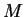 en un vecteur colonne
le vecteur de
en un vecteur colonne
le vecteur de 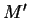 peut s'obtenir par l'action de la matrice
peut s'obtenir par l'action de la matrice
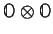 sur le vecteur colonne de
sur le vecteur colonne de 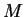 . Sachant que par exemple
. Sachant que par exemple
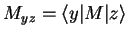 et connaissant la transformation unitaire reliant
et connaissant la transformation unitaire reliant
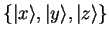 et
et
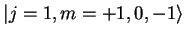 , montrer comment utiliser la table de Clebsch-Gordan
pour diagonaliser
, montrer comment utiliser la table de Clebsch-Gordan
pour diagonaliser
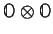 en 3 blocs carrés de
5, 3 et 1 dimensions. Vérifier en particulier que le bloc à une dimension correspond
bien à la combinaison invariante par rotation
Tr
en 3 blocs carrés de
5, 3 et 1 dimensions. Vérifier en particulier que le bloc à une dimension correspond
bien à la combinaison invariante par rotation
Tr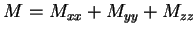 .
.


Next: Oscillations dans un système
Up: td00
Previous: td00
Jean Orloff
2001-01-08