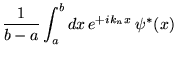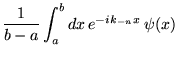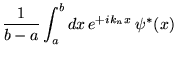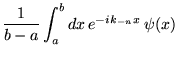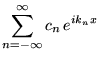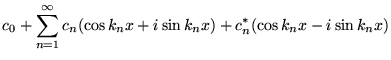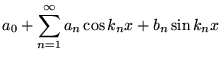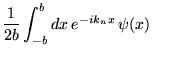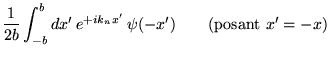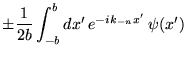suivant: 3.4 Questions rapides
monter: 3 Série de Fourier
précédent: 3.2 Convergence et Complétude
Table des matières
- Réalité:
- si
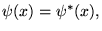 alors on a
alors on a
et donc:
On peut alors regrouper les termes de la série de Fourier complexe:
ce qui redonne la série de Fourier réelle avec
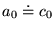 ,
,
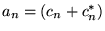 et
et
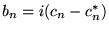 .
.
- Parité
- si la fonction possède une parité définie
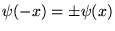 (on supposera de plus
(on supposera de plus 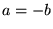 , pour que l'intervalle soit symétrique), alors
, pour que l'intervalle soit symétrique), alors
et donc
- Prolongement périodique
- on a besoin d'une fonction périodique pour pouvoir
développer en série de Fourier. C'est moins une restriction qu'il n'y parait,
puisqu'à partir de toute fonction
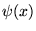 , on peut toujours définir
une fonction périodique
, on peut toujours définir
une fonction périodique
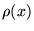 en répétant périodiquement la fonction
en répétant périodiquement la fonction
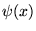 restreinte à l'intervalle
restreinte à l'intervalle ![$ [a,b] $](img203.gif) :
Ce prolongement introduit en général des discontinuités au bord pour
:
Ce prolongement introduit en général des discontinuités au bord pour 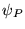 ou ses dérivées. De plus, l'information contenue dans les valeurs de
ou ses dérivées. De plus, l'information contenue dans les valeurs de 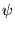 en dehors de l'intervalle sont irrémédiablement perdues quand on passe à
en dehors de l'intervalle sont irrémédiablement perdues quand on passe à 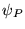 .
.




suivant: 3.4 Questions rapides
monter: 3 Série de Fourier
précédent: 3.2 Convergence et Complétude
Table des matières
2000-10-06