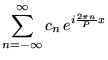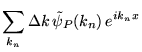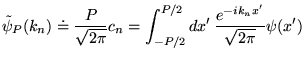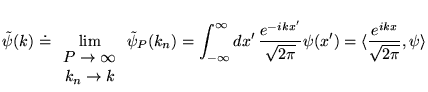suivant: 4.2 Transformations intégrales
monter: 4 Transformée de Fourier
précédent: 4 Transformée de Fourier
Table des matières
La série de Fourier peut se voir comme le développement dans une base de fonctions
propres de l'opérateur de dérivation 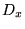 , mais reste limitée à des
fonctions périodiques. La généralisation à des fonctions non-périodiques porte
le nom de transformée de Fourier. Partant d'une fonction
, mais reste limitée à des
fonctions périodiques. La généralisation à des fonctions non-périodiques porte
le nom de transformée de Fourier. Partant d'une fonction 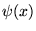 non-périodique
sur
non-périodique
sur
![$ x\in ]-\infty ,+\infty [ $](img519.gif) on peut construire la fonction
on peut construire la fonction
La fonction 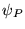 est ainsi de période
est ainsi de période 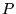 par construction
par construction
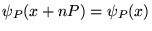 , et on peut donc la développer en série
de Fourier:
, et on peut donc la développer en série
de Fourier:
où dans la deuxième forme, on a simplement introduit les notations suggestives
et réécrit les coefficients de Fourier:
Si la fonction 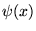 est sommable4.1, la fonction
existera et on appellera
est sommable4.1, la fonction
existera et on appellera
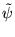 la transformée de Fourier
de
la transformée de Fourier
de 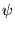 . Pour
. Pour
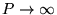 , la somme
, la somme
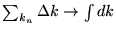 devient une intégrale, et on peut construire la fonction
devient une intégrale, et on peut construire la fonction
On voit donc que comme dans la série de Fourier, on est en train d'essayer de
développer 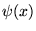 sur un ensemble de fonctions
sur un ensemble de fonctions
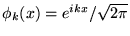 ,
sauf que cet ensemble est labellé par un ``indice''
,
sauf que cet ensemble est labellé par un ``indice'' 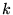 , tout aussi continu
que
, tout aussi continu
que 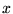 : on passe d'une ``base'' continue
: on passe d'une ``base'' continue 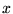 à une autre ``base''
continue
à une autre ``base''
continue 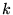 .
.




suivant: 4.2 Transformations intégrales
monter: 4 Transformée de Fourier
précédent: 4 Transformée de Fourier
Table des matières
2000-10-06
![]() , mais reste limitée à des
fonctions périodiques. La généralisation à des fonctions non-périodiques porte
le nom de transformée de Fourier. Partant d'une fonction
, mais reste limitée à des
fonctions périodiques. La généralisation à des fonctions non-périodiques porte
le nom de transformée de Fourier. Partant d'une fonction ![]() non-périodique
sur
non-périodique
sur
![]() on peut construire la fonction
on peut construire la fonction
![% latex2html id marker 16149
$\displaystyle \psi _{P}(x)=\left\{ \begin{array}{l...
...(-\frac{P}{2})] & \mathrm{si}\, \mathrm{x}=(n+\frac{1}{2})P
\end{array}\right. $](img520.gif)