



suivant: 5.2 Equations particulières du
monter: 5 Equations Différentielles
précédent: 5 Equations Différentielles
Table des matières
Pour la suite du cours, on va prendre le changement de notations suivant:
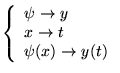
On appelle
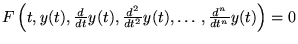 équation différentielle d'ordre
équation différentielle d'ordre 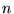 en la fonction
en la fonction 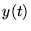
- Notation
-
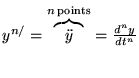
- Forme canonique
- on a résoudre en la dérivée d'ordre
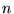 :
:
- Forme normale
- on se ramène à un système de
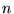 équations du
équations du 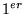 ordre:
ordre:
Toute forme canonique peut se ramener à cette forme par:
Exemple
Oscillateur harmonique:
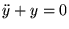
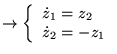
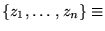 espace des phases (coordonnées
et vitesses généralisées)
espace des phases (coordonnées
et vitesses généralisées)
- Solution de l'équation différentielle
- (ou courbe intégrale)
Tout(e) (ensemble de) fonction(s) 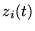 satisfaisant à l'équation
différentielle.
satisfaisant à l'équation
différentielle.
- Conditions aux limites
- À un moment
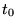 , on peut librement choisir
les
, on peut librement choisir
les
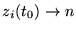 constantes d'intégration arbitraires: c'est
le problème de Cauchy ou problème aux conditions initiales (C.I.). On veut parfois
aussi remplacer des conditions au bord.
constantes d'intégration arbitraires: c'est
le problème de Cauchy ou problème aux conditions initiales (C.I.). On veut parfois
aussi remplacer des conditions au bord.
Exemple
Problème de tir.
On a un
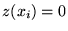 et un
et un
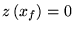 . En général,
c'est beaucoup plus compliqué et ce problème n'admet pas toujours une solution
(compatibilité des C.B.)
. En général,
c'est beaucoup plus compliqué et ce problème n'admet pas toujours une solution
(compatibilité des C.B.)
- Existence et unicité de la solution
- pour le problème de Cauchy.
Théorème
Si

est
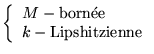
dans un même domaine
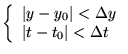
c'est-à-dire:
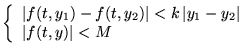
, alors
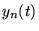
converge uniformément vers la solution unique, pour
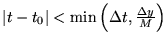
Preuve.
On montre que
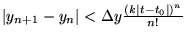
si
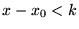
(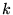 donne la vitesse de convergence)
donne la vitesse de convergence)

Remarque
Sur le théorème:
 pas pratique numériquement (on intègre pour chaque
pas pratique numériquement (on intègre pour chaque 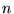 )
)
 se généralise pour le problème de Cauchy à
se généralise pour le problème de Cauchy à 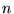 dimensions
dimensions




suivant: 5.2 Equations particulières du
monter: 5 Equations Différentielles
précédent: 5 Equations Différentielles
Table des matières
2000-10-06
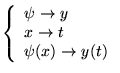
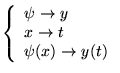
![]() équation différentielle d'ordre
équation différentielle d'ordre ![]() en la fonction
en la fonction ![]()
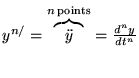
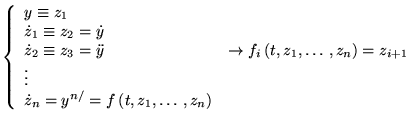
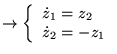
![]() espace des phases (coordonnées
et vitesses généralisées)
espace des phases (coordonnées
et vitesses généralisées)![]() et un
et un
![]() . En général,
c'est beaucoup plus compliqué et ce problème n'admet pas toujours une solution
(compatibilité des C.B.)
. En général,
c'est beaucoup plus compliqué et ce problème n'admet pas toujours une solution
(compatibilité des C.B.)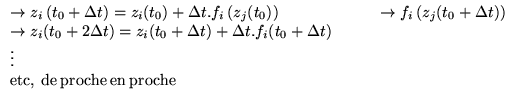
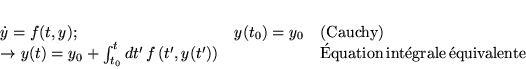
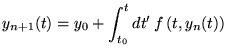
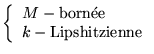 dans un même domaine
dans un même domaine
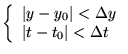 c'est-à-dire:
c'est-à-dire:
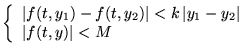 , alors
, alors ![]() donne la vitesse de convergence)
donne la vitesse de convergence)
![]()
![]() pas pratique numériquement (on intègre pour chaque
pas pratique numériquement (on intègre pour chaque ![]() )
)
![]() se généralise pour le problème de Cauchy à
se généralise pour le problème de Cauchy à ![]() dimensions
dimensions