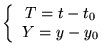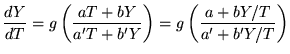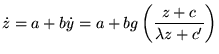


suivant: 5.3 Équations d'ordre supérieur
monter: 5 Equations Différentielles
précédent: 5.1 Introduction-Généralités
Table des matières
Sous-sections
Partons de la forme normale de l'équation du 1er ordre:
et envisageons différents cas où la solution s'obtient par quadrature (c'est-à-dire,
par des calculs de primitives).
On obtient une solution par simple intégration. Ou bien
ou bien
On peut tirer la fonction 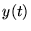 par l'égalité entre deux fonctions connues
par intégration de
par l'égalité entre deux fonctions connues
par intégration de
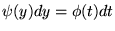
C'est une équation invariante sous
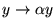 ;
;
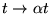 (multiplication de
(multiplication de 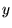 et
et 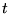 par la même constante). Posant comme
nouvelle inconnue
par la même constante). Posant comme
nouvelle inconnue
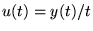 , on a
, on a
ce qui se ramène aux variables séparées.
Si
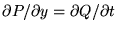 , il existe une fonction
, il existe une fonction
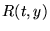 telle que
telle que
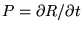 et
et
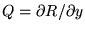 .
L'équation peut se réécrire comme une différentielle exacte:
.
L'équation peut se réécrire comme une différentielle exacte:
Les lignes du plan 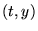 ou cette fonction
ou cette fonction 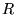 est constante en
sont donc des solutions. Pour construire la fonction
est constante en
sont donc des solutions. Pour construire la fonction 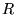 , il suffit de
connaître les primitives
, il suffit de
connaître les primitives
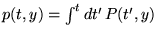 et
et
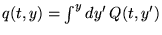 .
La solution de l'équation passant par un point
.
La solution de l'équation passant par un point
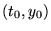 satisfait:
satisfait:
Remarque
Si
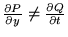
, on
peut essayer de trouver un facteur intégrant
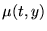
tel que
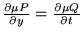
.
Un tel
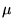
ne change pas l'équation de départ: on aura une solution
mais la recherche de ce
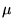
n'est pas simple en général:
Si 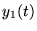 et
et 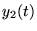 sont 2 solutions, alors
sont 2 solutions, alors
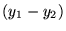 est solution de l'équation homogène (où
est solution de l'équation homogène (où 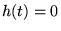 ). On cherche donc d'abord
la solution générale de cette équation homogène, c'est-à-dire le noyau de l'opérateur
différentiel
). On cherche donc d'abord
la solution générale de cette équation homogène, c'est-à-dire le noyau de l'opérateur
différentiel
Pour trouver une solution particulière 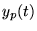 de l'équation non-homogène
(avec
de l'équation non-homogène
(avec 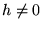 ), on cherche sous la forme (méthode de ``variation de
la constante''):
), on cherche sous la forme (méthode de ``variation de
la constante''):
La solution générale est donc
![% latex2html id marker 16686
$\displaystyle y(t;y_{0})=y_{0}e^{\int ^{t}_{t_{0}}...
..., g(t')}+\int _{t_{0}}^{t}d\tau \, h(\tau )\, e^{\int ^{t}_{\tau }dt'\, g(t')}]$](img690.gif) |
(5.2.1) |
dans laquelle 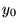 est la valeur (arbitraire) de la solution en
est la valeur (arbitraire) de la solution en 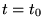 .
.
c'est une équation résolue en 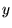 au lieu de
au lieu de 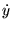 . Posons
. Posons
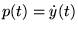 ,
et dérivons les deux membres de l'équation de départ par rapport à
,
et dérivons les deux membres de l'équation de départ par rapport à 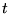 .
On obtient (avec les notations
.
On obtient (avec les notations
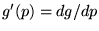 et
et
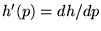 , deux
fonctions connues de
, deux
fonctions connues de 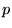 ):
):
Ceci est une équation linéaire en la fonction inconnue 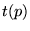 , que l'on
peut résoudre par la méthode générale vue plus haut (5.2.1). On obtient
la solution générale
, que l'on
peut résoudre par la méthode générale vue plus haut (5.2.1). On obtient
la solution générale
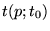 , où
, où 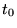 est la valeur prise
en un point
est la valeur prise
en un point 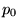 fixé arbitrairement. La courbe intégrale
fixé arbitrairement. La courbe intégrale 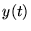 du problème de départ s'obtient alors sous forme paramétrique: lorsqu'on varie
du problème de départ s'obtient alors sous forme paramétrique: lorsqu'on varie
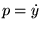 , la coordonnée
, la coordonnée 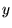 varie en vertu de l'équation de départ
comme
tandis que la coordonnée
varie en vertu de l'équation de départ
comme
tandis que la coordonnée 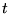 varie comme la solution de l'équation homogène:
En variant
varie comme la solution de l'équation homogène:
En variant 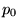 , on peut ajuster la valeur de la fonction
, on peut ajuster la valeur de la fonction
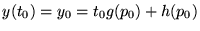 au point
au point 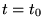 fixé.
fixé.
c'est le cas particulier de Lagrange où la fonction 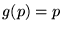 . En vertu
de (5.2.2), on a donc nécessairement
. En vertu
de (5.2.2), on a donc nécessairement 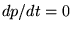 et
et 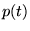 est une constante
est une constante 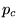 indépendante de
indépendante de 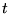 . Par conséquent, la
solution générale est une famille de droites
. Par conséquent, la
solution générale est une famille de droites
où pour chaque coefficient directeur 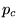 , l'ordonnée à l'origine est
dictée par la fonction
, l'ordonnée à l'origine est
dictée par la fonction 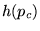 . Il faut remarquer que si
. Il faut remarquer que si 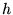 n'est
pas linéaire, il peut y avoir des points
n'est
pas linéaire, il peut y avoir des points
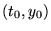 par lesquels aucune
courbe intégrale ne passe, ou au contraire, en lesquels plusieurs courbes se
croisent. Exemple: si
par lesquels aucune
courbe intégrale ne passe, ou au contraire, en lesquels plusieurs courbes se
croisent. Exemple: si
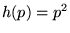 , il n'y aura aucune solution réelle
par le point
, il n'y aura aucune solution réelle
par le point 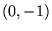 , mais deux droites de pente
, mais deux droites de pente 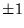 passant
par
passant
par 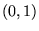 . Ceci découle de ce que l'équation ramenée sous forme normale
fait intervenir une fonction ayant deux branches (non univalue):
. Ceci découle de ce que l'équation ramenée sous forme normale
fait intervenir une fonction ayant deux branches (non univalue):
cette équation fait intervenir deux droites dans le plan 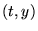 :
:
Il y a donc deux cas à envisager. Si les droites se croisent en un point
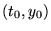 que l'on peut facilement déterminer en fonction des constantes
que l'on peut facilement déterminer en fonction des constantes
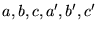 ,
on se ramène à une équation homogène en passant aux variables
,
on se ramène à une équation homogène en passant aux variables
Si par contre les droites sont parallèles, on doit avoir
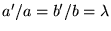 .
On peut alors poser
.
On peut alors poser
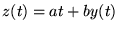 comme nouvelle fonction inconnue. Prenant
sa dérivée:
on retrouve une équation à variables séparées (indépendante de
comme nouvelle fonction inconnue. Prenant
sa dérivée:
on retrouve une équation à variables séparées (indépendante de 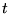 )
)



suivant: 5.3 Équations d'ordre supérieur
monter: 5 Equations Différentielles
précédent: 5.1 Introduction-Généralités
Table des matières
2000-10-06
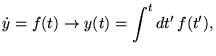
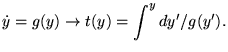
![]() par l'égalité entre deux fonctions connues
par intégration de
par l'égalité entre deux fonctions connues
par intégration de
![]()
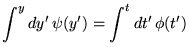
![]() ;
;
![]() (multiplication de
(multiplication de ![]() et
et ![]() par la même constante). Posant comme
nouvelle inconnue
par la même constante). Posant comme
nouvelle inconnue
![]() , on a
, on a
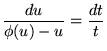
![]() , il existe une fonction
, il existe une fonction
![]() telle que
telle que
![]() et
et
![]() .
L'équation peut se réécrire comme une différentielle exacte:
.
L'équation peut se réécrire comme une différentielle exacte:
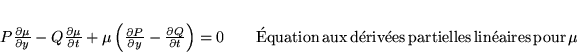
![]() et
et ![]() sont 2 solutions, alors
sont 2 solutions, alors
![]() est solution de l'équation homogène (où
est solution de l'équation homogène (où ![]() ). On cherche donc d'abord
la solution générale de cette équation homogène, c'est-à-dire le noyau de l'opérateur
différentiel
). On cherche donc d'abord
la solution générale de cette équation homogène, c'est-à-dire le noyau de l'opérateur
différentiel
![$\displaystyle \left[ \frac{d}{dt}-g(t)\right] y_{h}(t)=0$](img681.gif)
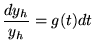
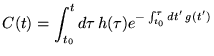
![]() au lieu de
au lieu de ![]() . Posons
. Posons
![]() ,
et dérivons les deux membres de l'équation de départ par rapport à
,
et dérivons les deux membres de l'équation de départ par rapport à ![]() .
On obtient (avec les notations
.
On obtient (avec les notations
![]() et
et
![]() , deux
fonctions connues de
, deux
fonctions connues de ![]() ):
):
![]() . En vertu
de (5.2.2), on a donc nécessairement
. En vertu
de (5.2.2), on a donc nécessairement ![]() et
et ![]() est une constante
est une constante ![]() indépendante de
indépendante de ![]() . Par conséquent, la
solution générale est une famille de droites
. Par conséquent, la
solution générale est une famille de droites
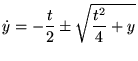
![]() :
: