![$\displaystyle L[y]\doteq \frac{d}{dt}\left[ \mu (t)\frac{d}{dt}y\right] +\mu q(t)=-\lambda p(t)y(t)$](img962.gif)
On prend une équation linéairement indépendante et homogène du second degré, sous la forme:
![$\displaystyle L[y]\doteq \frac{d}{dt}\left[ \mu (t)\frac{d}{dt}y\right] +\mu q(t)=-\lambda p(t)y(t)$](img962.gif)
avec
![% latex2html id marker 17506
$ \left\{ \begin{array}{l}
\mu (t),q(t)\textrm{ et ...
...extrm{elles et continues sur }[a,b]\\
\mu (t)>0,\, p(t)>0
\end{array}\right. $](img963.gif)
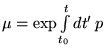
![]() la restriction à
la restriction à ![]() équivaut à pas de point singulier
dans
équivaut à pas de point singulier
dans ![]()
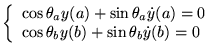
Les valeurs de ![]() (paramètre complexe) pour lesquelles c'est possible
sont des valeurs propres, et les
(paramètre complexe) pour lesquelles c'est possible
sont des valeurs propres, et les
![]() associées sont des
fonctions propres. L'ensemble des valeurs propres constitue le spectre
de
associées sont des
fonctions propres. L'ensemble des valeurs propres constitue le spectre
de ![]() pour ces CL, il est généralement discret.
pour ces CL, il est généralement discret.
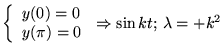 avec
avec
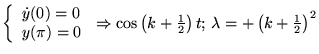 avec
avec
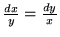 avec
avec