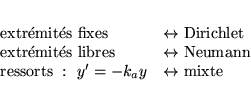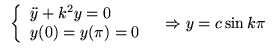suivant: 6.1 Problème de Sturm-Liouville
monter: Licence de Physique: Opérateurs
précédent: 5.6 Points singuliers irréguliers
Table des matières
Jusqu'ici, on s'était intéressé à des problèmes de Cauchy (ie: CI):
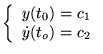
On va regarder:
-
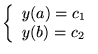 (problème de Dirichlet)
(problème de Dirichlet)
-
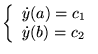 (problème de Neuman)
(problème de Neuman)
-
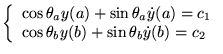 (problème mixte)
(problème mixte)
Exemple
Applications physiques:
- Corde vibrante:
- Problèmes ballistiques, rendez-vous spatiaux,
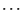
- Problème
- Même si
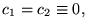 la solution n'est pas nécessairement
unique
la solution n'est pas nécessairement
unique
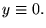 On peut en effet prendre par exemple:
On peut en effet prendre par exemple:
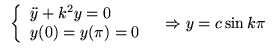
Il y a donc une différence fondamentale avec les problèmes de Cauchy où on avait
un théorème d'unicité. C'est une différence TRÈS féconde grâce au théorème de
développement (Fourier généralisé).
Sous-sections
2000-10-06
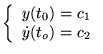
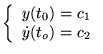
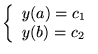 (problème de Dirichlet)
(problème de Dirichlet)
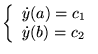 (problème de Neuman)
(problème de Neuman)
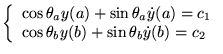 (problème mixte)
(problème mixte)