


suivant: 7 Équations aux dérivées
monter: 6 Problèmes aux bords
précédent: 6.1 Problème de Sturm-Liouville
Table des matières
Sous-sections
Si 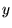 et
et 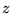 sont des fonctions
sont des fonctions
![$ \dot{y},L[y]\in C^{0}[a,b] $](img978.gif) :
:
avec
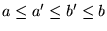
- Conséquences
-
- Propriétés
-
- Application
- Problème non-homogène.
Preuve.
=\int _{a}^{b}d\tau \, \underbrace{L_{t}[G(t,\tau )]}_{-\delta (t-\tau )}g(\tau )=-g(t) $](img998.gif)
ce qui démontre la partie ``nécessaire''. On a la formule de Green avec
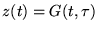
(on a en effet
![$ [\mu W_{2}]_{a}^{b}=0 $](img1000.gif)
car on a les mêmes CL) pour démontrer
la partie ``suffisante''.

- Analogie
-
 est la fonction de Green du laplacien scalaire
est la fonction de Green du laplacien scalaire
La fonction de Green est la réponse à une source ponctuelle 
Exemple
Si
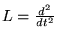
On prend
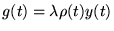 d'où
d'où
![% latex2html id marker 17627
$ L[y]=-\lambda \rho y\Leftrightarrow \int ^{b}_{a}d\tau \, G(t,\tau )\rho (\tau )y(\tau )=\frac{1}{\lambda }y(t) $](img1009.gif)
On pose
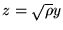 ;
;
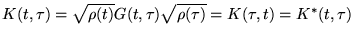
d'où:
``
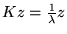 '' est une notation abrégée pour dire que l'opérateur
'' est une notation abrégée pour dire que l'opérateur
 est hermitien.
est hermitien.
- Propriétés
-
Remarque
Les fonctions propres
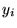
de
![$ L[y_{i}]=\lambda _{i}y_{i} $](img1026.gif)
ont
un produit scalaire
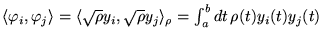
Remarque
Seules les fonctions
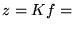
image de
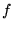
par
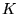
sont développables.
Si
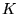
ne contient que
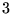
vecteurs propres, (noyau dégénéré), ça
marche trivialement.
Si
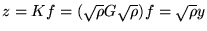 alors
alors 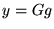 avec
avec
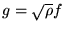
Donc si 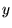 solution de
solution de ![$ L[y]=-\nu $](img1032.gif) avec des CL déterminées et
avec des CL déterminées et
![$ \nu \in C_{[a,b]}^{0} $](img1033.gif) alors:
alors:
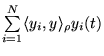 convergeras
uniformément vers
convergeras
uniformément vers 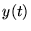 .
.
Remarque
Ceci n'impose presqu'aucune restriction sur
: connaissant
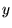
,
je peux calculer
![$ L[y]=-\nu $](img1032.gif)
qui doit être simplement
!
 Il suffit que
Il suffit que
![$ y\in C^{0}_{[a,b]} $](img1035.gif)
Ceci s'applique aussi aux polynômes orthogonaux et aux fonctions de Bessel.



suivant: 7 Équations aux dérivées
monter: 6 Problèmes aux bords
précédent: 6.1 Problème de Sturm-Liouville
Table des matières
2000-10-06
![]() et
et ![]() sont des fonctions
sont des fonctions
![]() :
:
![$\displaystyle \frac{d}{dt}\left[ \mu \underbrace{(y\dot{z}-z\dot{y})}_{W_{2}(y,z;t)}\right] =yL[z]-zL[y]+\mu (\dot{y}\dot{z}-\dot{z}\dot{y})-\mu q(yz-zy)$](img979.gif)
![% latex2html id marker 17556
$\displaystyle \rightarrow [\mu W_{2}(y,z;t)]_{a'}^{b'}=\int _{a'}^{b'}dt\, (yL[z]-zL[y])\qquad \textrm{Formule de Green}$](img980.gif)
![]()
![% latex2html id marker 17578
$ \left\{ \begin{array}{l}
L[y_{1}]=0;\quad \cos \t...
...d \cos \theta _{b}y_{2}(b)+\sin \theta _{b}\dot{y}_{2}(b)=0
\end{array}\right. $](img988.gif) alors
alors
![% latex2html id marker 17582
$\displaystyle \rightarrow \begin{array}{ll}
\boxed...
...y}\right. }& \textrm{Fonction de Green pour }L[y],\textrm{ avec CL}
\end{array}$](img990.gif)
![\begin{displaymath}
% latex2html id marker 17592\begin{array}{l}
=-\frac{1}{\m...
...\tau )))=\boxed{L_{t}[G(t,\tau )]=-\delta (t-\tau )}\end{array}\end{displaymath}](img995.gif)
![% latex2html id marker 17598
$\displaystyle \left\{ \begin{array}{l}
L[y]=-g(t)\...
...rrow y(t)=\int _{a}^{b}d\tau \, G(t,\tau )g(\tau )\qquad \textrm{est solution}.$](img997.gif)
=\int _{a}^{b}d\tau \, \underbrace{L_{t}[G(t,\tau )]}_{-\delta (t-\tau )}g(\tau )=-g(t) $](img998.gif) ce qui démontre la partie ``nécessaire''. On a la formule de Green avec
ce qui démontre la partie ``nécessaire''. On a la formule de Green avec
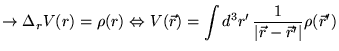
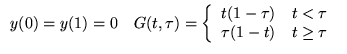
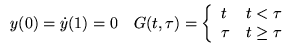
![]() d'où
d'où
![]()
![]() ;
;
![]()
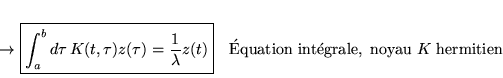
![]() '' est une notation abrégée pour dire que l'opérateur
'' est une notation abrégée pour dire que l'opérateur
![]() est hermitien.
est hermitien.
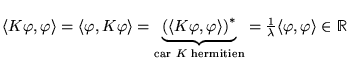 .
.
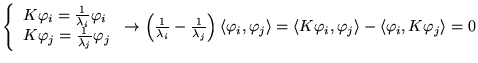
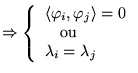
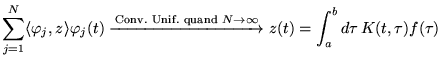
![]() alors
alors ![]() avec
avec
![]()
![]() solution de
solution de ![]() avec des CL déterminées et
avec des CL déterminées et
![]() alors:
alors:
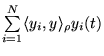 convergeras
uniformément vers
convergeras
uniformément vers ![]() .
.
![]() Il suffit que
Il suffit que
![]()