7.1 Définitions

7.1.1 Forme générale:

relation liant une fonction inconnue de $n$ variables $z(x_{1},\ldots x_{n})=z(\vec{x})$ à ses dérivées partielles, notées en abrégé:

$$\partial _{i}z \doteq \frac{\partial z}{\partial x_{i}}=\lim _{\epsilon \rightarrow 0}\... ...(x_{1},\ldots x_{i}+\epsilon ,\ldots x_{n})-z(x_{1},\ldots x_{i},\ldots x_{n})]$$

$$\partial _{i}\partial _{j}z \doteq \frac{\partial ^{2}z}{\partial x_{i}\partial x_{j}}$$

$$F(x_{1},x_{2},\ldots x_{n},z,\partial _{1}z,\ldots \partial _{n}z,\ldots ,\partial _{1}^{k_{1}}\ldots \partial _{n}^{k_{n}}z,\ldots )=0$$ (7.1.1)

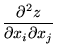où la dernière expression représente la fonction $z$ dérivée $k_{1}$ fois par rapport à $x_{1}$, $k_{2}$ fois par rapport à $x_{2}$ et $k_{n}$ fois par rapport à $x_{n}$; c'est donc une dérivée partielle d'ordre $k_{1}+k_{2}+\cdots k_{n}$. Comme d'habitude, l'ordre d'une équation aux dérivées partielles est l'ordre le plus élévé des dérivées partielles apparaissant dans l'équation.

Exemples pour une fonction de 2 variables: $z=z(x,y)$:

1er ordre:	$\partial _{x}z=0$	$\rightarrow z=f(y)$	une fonction arbitraire
2e ordre:	$\partial _{x}\partial _{y}z=0$	$\rightarrow \partial _{y}z=f'(y)$
		$\rightarrow z=f(x)+g(y)$	2 fonctions arbitraires
1er ordre (N.L.)	$(\partial _{x}z)^{2}+(\partial _{y}z)^{2}=0$	$\rightarrow z=cte$
``& $(\partial _{x}z)^{2}+(\partial _{y}z)^{2}+1=0$	pas de sol. réelle

7.1.2 EDP Linéaire

On se limitera dans la suite aux EDPL (valable pour pour des faibles amplitudes ``$z\ll 1$''). La forme générale d'une EDPL est

$$L[z]=f(\vec{x})$$ (7.1.2)

avec un opérateur différentiel linéaire

$$L[z]=[p(\vec{x})+\sum ^{n}_{i=1}p_{i}(\vec{x})\partial _{i}+\sum ^{n}_{i,j=1}p_{ij}(\vec{x})\partial _{i}\partial _{j}+\cdots ]z(\vec{x})$$ (7.1.3)

caractérisé par des fonctions données de $n$ variables $p_{i}(\vec{x}),p_{ij}(\vec{x}),\ldots$

7.1.3 EDPL Homogène:

L'EDPL est homogène si la fonction $f(\vec{x})$ pouvant appaître dans le second membre est la fonction nulle. Dans ce cas, si on connaît $d$ solutions indépendantes $z_{1}(\vec{x}),z_{2}(\vec{x}),\ldots z_{d}(x)$, on a automatiquement tout un espace vectoriel à $d$ dimensions de solutions:

$$L\left[ \sum ^{d}_{\alpha =1}c_{\alpha }z_{\alpha }(\vec{x})\right] =\sum ^{d}_{\alpha =1}c_{\alpha }L[z_{\alpha }(\vec{x})]=0$$