On essaie de trouver un
![]() de la forme:
de la forme:
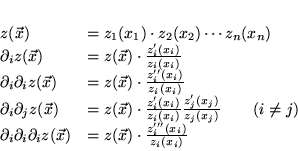
![]() aura une solution à séparation de variables si: (restrictions
sur
aura une solution à séparation de variables si: (restrictions
sur ![]() )
)
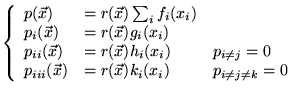
d'où
![$ \displaystyle L[z]=r(\vec{x})z(\vec{x})\sum ^{n}_{i=1}\underbrace{\left( f_{i}...
...{1}{z_{i}(x_{i})}L_{i}[z_{i}]=\textrm{fonction de }x_{i}\textrm{ seulement}}=0 $](img1068.gif)
Pour chaque ![]() , on doit avoir:
, on doit avoir:
![$\displaystyle \left\{ \begin{array}{l}
\displaystyle \frac{1}{z_{i}}L_{i}[z_{i}]=\lambda _{i}=cte_{i}\\
\sum ^{n}_{i=1}\lambda _{i}=0
\end{array}\right. $](img1070.gif)
![]() Pour chaque variable, on a une équation différentielle aux
valeurs propres:
Pour chaque variable, on a une équation différentielle aux
valeurs propres:
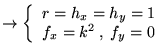
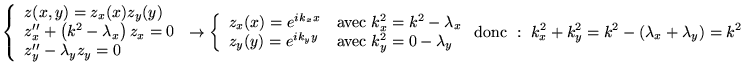
d'où
![]() avec toujours
avec toujours
![]() .
.