



suivant: 7.5 Équations hyperboliques
monter: 7 Équations aux dérivées
précédent: 7.3 EDPL du premier
Table des matières
Pour simplifier, prenons 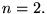
- Question
- Quelles sont les conditions initiales?
Essayons de donner
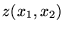 sur courbe
sur courbe 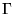 et voyons
ce qui manque. On connaît la dérivée tangentielle le long de la courbe
et voyons
ce qui manque. On connaît la dérivée tangentielle le long de la courbe 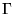 :
:
Donnons-nous 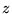 et
et
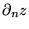 sur
sur 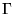 : on connaît
alors
: on connaît
alors
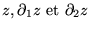 sur
sur 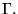
Intéressons maintenant aux dérivées d'ordre 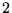 ; on en connaît
; on en connaît 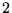 sur
sur 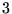 :
:
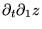 et
et
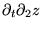 .
Pour la
.
Pour la
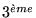 , on peut essayer d'utiliser l'équation homogène:
, on peut essayer d'utiliser l'équation homogène:
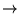 Possible si
Possible si 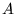 est réversible, c'est-à-dire:
est réversible, c'est-à-dire:
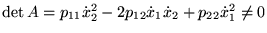
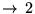 ED: en chaque point du plan
ED: en chaque point du plan
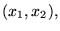 on
a une valeur dangereuse de
on
a une valeur dangereuse de
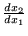
 familles de courbes intégrales dans le plan: courbes
caractéristiques.
familles de courbes intégrales dans le plan: courbes
caractéristiques.
- Interprétation
- Le déterminant de
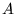 est le coefficient de
est le coefficient de
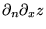 dans l'équation homogène.
dans l'équation homogène.
Si
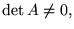 on peut alors toujours exprimer sur
on peut alors toujours exprimer sur 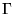 :
:




suivant: 7.5 Équations hyperboliques
monter: 7 Équations aux dérivées
précédent: 7.3 EDPL du premier
Table des matières
2000-10-06
![\begin{displaymath}
% latex2html id marker 17913\begin{array}{lr}
L[z]=\left[ ...
...textrm{quation homog}\grave{\textrm{e}}\textrm{ne})
\end{array}\end{displaymath}](img1101.gif)
![\begin{displaymath}
% latex2html id marker 17913\begin{array}{lr}
L[z]=\left[ ...
...textrm{quation homog}\grave{\textrm{e}}\textrm{ne})
\end{array}\end{displaymath}](img1101.gif)
![]()
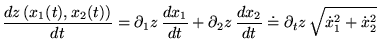
![]() et
et
![]() sur
sur ![]() : on connaît
alors
: on connaît
alors
![]() sur
sur ![]()
![]() ; on en connaît
; on en connaît ![]() sur
sur ![]() :
:
![]() et
et
![]() .
Pour la
.
Pour la
![]() , on peut essayer d'utiliser l'équation homogène:
, on peut essayer d'utiliser l'équation homogène:
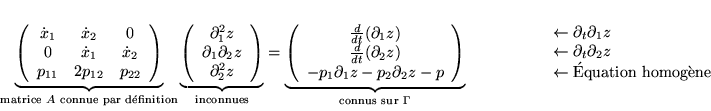
![]() Possible si
Possible si ![]() est réversible, c'est-à-dire:
est réversible, c'est-à-dire:
![]()

![]() ED: en chaque point du plan
ED: en chaque point du plan
![]() on
a une valeur dangereuse de
on
a une valeur dangereuse de
![]()
![]() familles de courbes intégrales dans le plan: courbes
caractéristiques.
familles de courbes intégrales dans le plan: courbes
caractéristiques.

