



suivant: 7.6 Équations elliptiques: (électrostatique)
monter: 7 Équations aux dérivées
précédent: 7.4 EDPL du second
Table des matières
Sous-sections
7.5 Équations hyperboliques
Pour 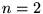 , on a
, on a 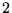 courbes caractéristiques différentes par chaque
point
courbes caractéristiques différentes par chaque
point
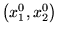 :
:
En faisant le changement de variables
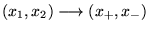 on peut montrer que:
on peut montrer que:
Supposons
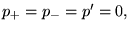 et faisons un autre changement de variables:
et faisons un autre changement de variables:
On a alors 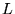 qui s'exprime sous la forme:
qui s'exprime sous la forme:
![$ L[z]=\frac{1}{4}\left( \partial _{t}+\partial _{+}\left) \right( -\partial _{t}+\partial _{x}\right) z $](img1129.gif)
- SGEH
-
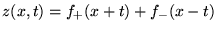
- Condition de Cauchy
- Si on se donne:
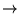 on peut déterminer
on peut déterminer 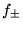 en termes de C.I.:
en termes de C.I.:
d'où:
- Fonction de Green ``retardée''
-
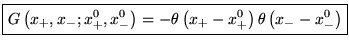
Solution de
![% latex2html id marker 18015
$ \left\{ \begin{array}{ll}
L[G]=-\delta \left( x_{...
..._{0}) & \\
\forall t<t_{0}\, :\, G,\, \partial _{t}G=0 &
\end{array}\right. $](img1137.gif)
Effet d'une force extérieure localisée en
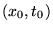 sur une corde
initialement au repos (marteau de piano
sur une corde
initialement au repos (marteau de piano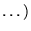 . N'a d'effet qu'à l'intérieur
du cône futur (causalité).
. N'a d'effet qu'à l'intérieur
du cône futur (causalité).
Exemple
corde vibrante à extrêmités fixes:
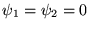
.
Solution: on développe sur une base des solutions de l'opérateur spatial (Fourier).
On obtient la SGEH par superposition (Sturm-Liouville)
- Unicité de la solution
-
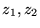 sont deux solutions différentes avec
les mêmes
sont deux solutions différentes avec
les mêmes
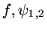 et
et
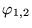 . Par superposition,
on peut alors construire une troisième solution
. Par superposition,
on peut alors construire une troisième solution 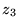 telle que:
telle que:
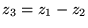 pour laquelle on a
pour laquelle on a
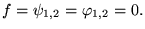 Pour montrer que
Pour montrer que
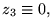 on construit l'énergie conservée d'une solution de l'équation homogène:
on construit l'énergie conservée d'une solution de l'équation homogène:
Si de plus
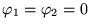 alors
alors
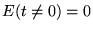 et
et
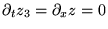 donc
donc 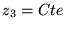 . Or d'après
les conditions aux bords,
. Or d'après
les conditions aux bords,
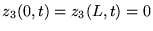 donc
donc
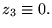
Il se peu a priori qu'on ne trouve pas de solutions pour des
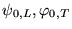 arbitraires: c'est un problème mal posé.
arbitraires: c'est un problème mal posé.
Preuve.
Contre-exemple à partir de SGEH: pour
![$ \tau \in [0,\min (L,T)], $](img1158.gif)
on a:
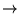 incompatible (par exemple si
incompatible (par exemple si 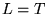 )
)





suivant: 7.6 Équations elliptiques: (électrostatique)
monter: 7 Équations aux dérivées
précédent: 7.4 EDPL du second
Table des matières
2000-10-06
![]() , on a
, on a ![]() courbes caractéristiques différentes par chaque
point
courbes caractéristiques différentes par chaque
point
![]() :
:
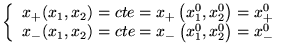
![]() on peut montrer que:
on peut montrer que:
![\begin{displaymath}
% latex2html id marker 17989\begin{array}{ll}
L[z]=\partia...
...+p'(x_{+},x_{-})z=0 & \qquad \textrm{Forme normale}
\end{array}\end{displaymath}](img1126.gif)
![]() et faisons un autre changement de variables:
et faisons un autre changement de variables:
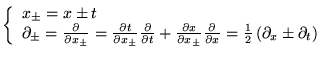
![]() qui s'exprime sous la forme:
qui s'exprime sous la forme:
![]()
![\begin{displaymath}
% latex2html id marker 17999\begin{array}{ll}
\boxed{L[z]=...
... \acute{\textrm{E}}\textrm{quation d}'\textrm{onde}
\end{array}\end{displaymath}](img1130.gif)
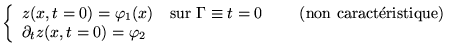
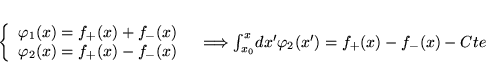
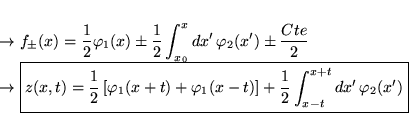
![% latex2html id marker 18015
$ \left\{ \begin{array}{ll}
L[G]=-\delta \left( x_{...
..._{0}) & \\
\forall t<t_{0}\, :\, G,\, \partial _{t}G=0 &
\end{array}\right. $](img1137.gif)
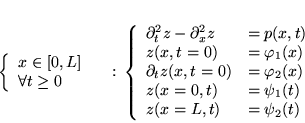
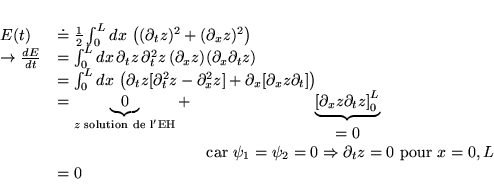
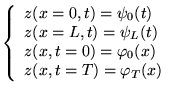
![]() arbitraires: c'est un problème mal posé.
arbitraires: c'est un problème mal posé.
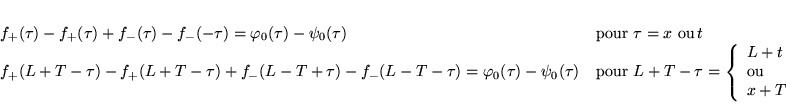
![]() incompatible (par exemple si
incompatible (par exemple si ![]() )
)
![]()