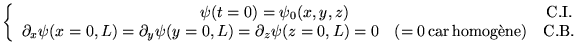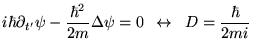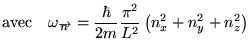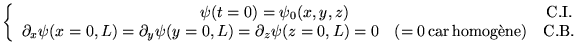suivant: 1.4 Questions rapides
monter: 1 Introduction: Refroidissement d'un
précédent: 1.2 Résolution
Table des matières
- Les
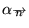 sont tous positifs, toutes les exponentielles
sont donc décroissantes
sont tous positifs, toutes les exponentielles
sont donc décroissantes
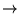 problème bien posé: pas d'amplification exponentielle d'une
incertitude sur les C.I. (du type ``effet papillon'')
problème bien posé: pas d'amplification exponentielle d'une
incertitude sur les C.I. (du type ``effet papillon'')
-
 : il y a un trou entre
la valeur la plus basse de
: il y a un trou entre
la valeur la plus basse de 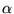 et la suivante (spectre discret).
Ceci vient de ce que
et la suivante (spectre discret).
Ceci vient de ce que 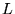 est fini. Grâce à quoi, si on attend
suffisament longtemps, est sûr de la forme spatiale de la distribution
de température:
et ce, indépendamment de la condition initiale
est fini. Grâce à quoi, si on attend
suffisament longtemps, est sûr de la forme spatiale de la distribution
de température:
et ce, indépendamment de la condition initiale 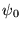 (qui ne détermine
que
(qui ne détermine
que 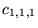 )
)
- Si au lieu de se donner la température au bord, on fixe le flux de chaleur
dans la direction normale au bord
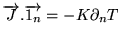 ,
il faut alors trouver une autre solution particulière
,
il faut alors trouver une autre solution particulière
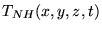 .
On définira ensuite
.
On définira ensuite
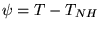 qui sera solution de la même
équation avec:
qui sera solution de la même
équation avec:
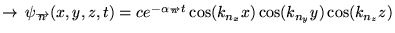 avec
avec
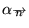 défini comme précédemment.
défini comme précédemment.
Exemple concret: dans le problème précédant d'une température
initiale uniforme, on a
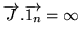 en
en 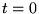 . Ceci est irréaliste: un bain thermique ne peut extraire plus
qu'un certain flux de chaleur maximum
. Ceci est irréaliste: un bain thermique ne peut extraire plus
qu'un certain flux de chaleur maximum 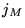 . Dans ce cas, on aura
du moins au début, tant que
. Dans ce cas, on aura
du moins au début, tant que
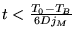
- Si on prolonge
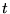 en une variable complexe, que l'on pose
en une variable complexe, que l'on pose 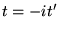 et que l'on s'intéresse à des valeurs réelles de
et que l'on s'intéresse à des valeurs réelles de 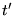 (rotation
de Wick), l'équation de la chaleur devient l'équation de Schroedinger
pour une particule libre dans un cube:
avec des oscillations temporelles (non amorties à la limite où
(rotation
de Wick), l'équation de la chaleur devient l'équation de Schroedinger
pour une particule libre dans un cube:
avec des oscillations temporelles (non amorties à la limite où 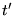 est
exactement réel)
est
exactement réel)
- L'équation d'onde
dans laquelle
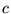 est une vitesse de propagation (p.ex. du son), possède
des solutions similaires, simplement :
avec
est une vitesse de propagation (p.ex. du son), possède
des solutions similaires, simplement :
avec
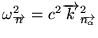 déterminant les fréquences de résonnances dans une pièce cubique où
déterminant les fréquences de résonnances dans une pièce cubique où
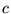 est la vitesse du son dans l'air.
est la vitesse du son dans l'air.




suivant: 1.4 Questions rapides
monter: 1 Introduction: Refroidissement d'un
précédent: 1.2 Résolution
Table des matières
2000-10-06