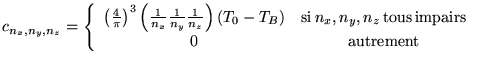suivant: 1.3 Remarques
monter: 1 Introduction: Refroidissement d'un
précédent: 1.1 Equation de la
Table des matières
Sous-sections
1.2.1 Homogénéité des C.B.
Les conditions au bord ne sont pas homogènes: si 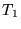 est solution,
est solution,
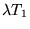 aura au bord
aura au bord
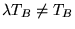 . On cherche
donc d'abord une solution particulière pour ces conditions au bord, par exemple:
. On cherche
donc d'abord une solution particulière pour ces conditions au bord, par exemple:
On passe ensuite à une nouvelle inconnue:
avec
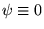 au bord du cube
au bord du cube
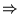
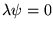 au bord aussi (homogène). Le problème devient donc
au bord aussi (homogène). Le problème devient donc
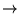
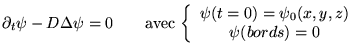 |
(1.2.1) |
On cherche des solutions particulières de cette forme, d'où:
Donc l'équation (1.2.1) s'écrit:
Comme
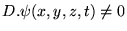 , et que chaque terme du crochet ne dépend
que de sa variable, chacun doit être constant et on a:
, et que chaque terme du crochet ne dépend
que de sa variable, chacun doit être constant et on a:
Ces conditions aux bords sont séparables: pour assurer
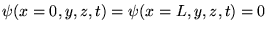 ,
il suffit par exemple de demander
,
il suffit par exemple de demander
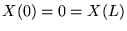 . Ceci empêche la constante
. Ceci empêche la constante
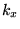 de prendre des valeurs continues arbitraires:
de prendre des valeurs continues arbitraires:
De même pour 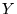 et
et 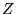 :
:
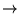 pour chaque triplet d'entiers
pour chaque triplet d'entiers
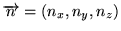 ,
on a 1 solution:
,
on a 1 solution:
avec
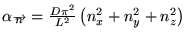
Figure:
Section dans le plan
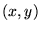 des premières solutions
du type (1.2.2).
des premières solutions
du type (1.2.2).
|
|
Chaque choix de
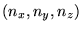 correspond à des conditions
initiales
correspond à des conditions
initiales
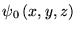 différentes. Comme l'équation
pour
différentes. Comme l'équation
pour 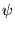 est linéaire et homogène, et que les conditions au bord du
cube (
est linéaire et homogène, et que les conditions au bord du
cube (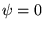 Cf 1.2.1) sont homogènes,
toutes combinaison linéaire
Cf 1.2.1) sont homogènes,
toutes combinaison linéaire
sera également solution pour n'importe quel choix des constantes
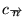 dépendant de 3 indices
dépendant de 3 indices
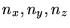 , et correspondra à des conditions
initiales différentes. Nous verrons dans le cours les propriétés étonnantes
suivantes:
, et correspondra à des conditions
initiales différentes. Nous verrons dans le cours les propriétés étonnantes
suivantes:
- toute condition initiale (``suffisament gentille'') peut s'écrire de la sorte
(
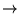 on écrit ``toute'' fonction de 3 variables comme somme
de produits de fonctions d'une variable!)
on écrit ``toute'' fonction de 3 variables comme somme
de produits de fonctions d'une variable!)
- cette décomposition est unique!
Pour une température initiale uniforme 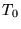 ,
,
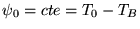 ,
nous verrons par série de Fourier que les constantes à prendre sont:
,
nous verrons par série de Fourier que les constantes à prendre sont:
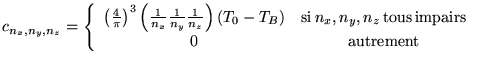




suivant: 1.3 Remarques
monter: 1 Introduction: Refroidissement d'un
précédent: 1.1 Equation de la
Table des matières
2000-10-06
![]() est solution,
est solution,
![]() aura au bord
aura au bord
![]() . On cherche
donc d'abord une solution particulière pour ces conditions au bord, par exemple:
. On cherche
donc d'abord une solution particulière pour ces conditions au bord, par exemple:
![]()
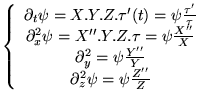
![% latex2html id marker 14882
$\displaystyle (-D)\psi (x,y,z,t).\left[ -\frac{1}{...
...{X''}{X}(x)+\frac{Y''}{Y}(y)+\frac{Z''}{Z}(z)\right] =0\quad \forall \, x,y,z,t$](img78.gif)
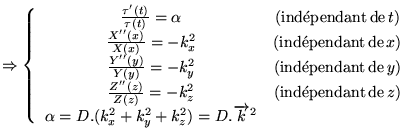
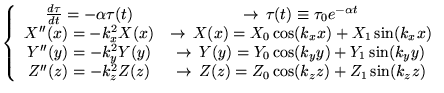
![]() ,
il suffit par exemple de demander
,
il suffit par exemple de demander
![]() . Ceci empêche la constante
. Ceci empêche la constante
![]() de prendre des valeurs continues arbitraires:
de prendre des valeurs continues arbitraires:
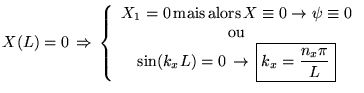 avec
avec
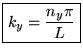 avec
avec
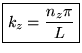 avec
avec
![]()
![]() correspond à des conditions
initiales
correspond à des conditions
initiales
![]() différentes. Comme l'équation
pour
différentes. Comme l'équation
pour ![]() est linéaire et homogène, et que les conditions au bord du
cube (
est linéaire et homogène, et que les conditions au bord du
cube (![]() Cf 1.2.1) sont homogènes,
toutes combinaison linéaire
Cf 1.2.1) sont homogènes,
toutes combinaison linéaire
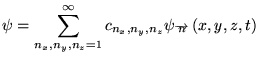
![]() ,
,
![]() ,
nous verrons par série de Fourier que les constantes à prendre sont:
,
nous verrons par série de Fourier que les constantes à prendre sont: