
Next: About this document ...
Up: td00
Previous: L'atome d'Hélium
On a vu précédemment par l'étude perturbative au 2e ordre en
| |
|
 |
(5) |
| |
|
![$\displaystyle \Rightarrow E_{n}(\lambda _{3})=\hbar \omega [n+\frac{1}{2}+\frac{\lambda _{3}^{2}}{4}(-15n^{2}-15n-2)+O(\lambda _{3}^{4})],$](img288.gif) |
(6) |
et on a noté que pour
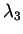 fixé,
fixé, 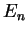 décroissait indéfiniment
à grand
décroissait indéfiniment
à grand 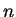 . Comme le potentiel classique
. Comme le potentiel classique
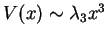 est non-borné inférieurement à grand
est non-borné inférieurement à grand 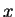 , on ne peut savoir si cette propriété
des
, on ne peut savoir si cette propriété
des 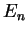 est un artefact de l'approche perturbative, ou un problème
inévitable du potentiel choisi. Pour le savoir, on va ajouter un terme
est un artefact de l'approche perturbative, ou un problème
inévitable du potentiel choisi. Pour le savoir, on va ajouter un terme
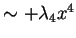 qui stabilise le potentiel, et calculer son effet au premier ordre sur
qui stabilise le potentiel, et calculer son effet au premier ordre sur 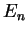 .
.
- Étude classique du potentiel:7
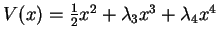
Montrer que pour
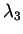 fixé, il y 2 valeurs critiques de
fixé, il y 2 valeurs critiques de
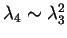 :
l'une8 au-dessous de laquelle apparaît un second minimum, et l'autre9 au-dessous de laquelle ce second minimum possède une énergie potentielle inférieure
à
:
l'une8 au-dessous de laquelle apparaît un second minimum, et l'autre9 au-dessous de laquelle ce second minimum possède une énergie potentielle inférieure
à 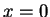 . Quelle symétrie apparaît pour cette seconde valeur critique? Comment
se comporte la position du second minimum lorsque
. Quelle symétrie apparaît pour cette seconde valeur critique? Comment
se comporte la position du second minimum lorsque
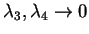 avec
avec
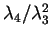 fixé?
fixé?
- Niveaux d'énergie perturbatifs: calculer les niveaux d'énergies à des
termes d'ordre
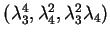 près.10. Le problème à grand
près.10. Le problème à grand 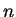 a-t-il disparu pour toutes les valeurs de
a-t-il disparu pour toutes les valeurs de
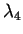 ?
Pouvez-vous croire au résultat obtenu pour
?
Pouvez-vous croire au résultat obtenu pour
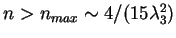 ?
?
- Approche variationnelle: Si le potentiel possède 2 minima, on peut
l'assimiler à un oscillateur harmonique au voisinage de chacun d'eux. Les opérateurs
de création
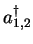 créeront alors 2 ``tours'' d'états indépendantes.
Montrer que pour
créeront alors 2 ``tours'' d'états indépendantes.
Montrer que pour
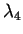 suffisamment petit, les intégrales de recouvrement
seront négligeables, et ces états seront pratiquement orthogonaux. Si l'on a
dégénérescence exacte entre les 2 minima (p.ex, par argument de symétrie), ces
termes de recouvrement bien que petits, lèvent cette dégénérescence. Quel est
l'ordre de grandeur en fonction de
suffisamment petit, les intégrales de recouvrement
seront négligeables, et ces états seront pratiquement orthogonaux. Si l'on a
dégénérescence exacte entre les 2 minima (p.ex, par argument de symétrie), ces
termes de recouvrement bien que petits, lèvent cette dégénérescence. Quel est
l'ordre de grandeur en fonction de
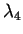 de la différence d'énergie?
Peut-on trouver cet effet à un ordre fini de l'approche perturbative?
de la différence d'énergie?
Peut-on trouver cet effet à un ordre fini de l'approche perturbative?
- Limite semi-classique: Pour
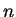 grand, on doit retrouver la règle
de quantification de Bohr-Sommerfeld. Pour chaque énergie classique
grand, on doit retrouver la règle
de quantification de Bohr-Sommerfeld. Pour chaque énergie classique 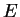 ,
il existe 2 points
,
il existe 2 points
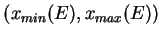 limitant la zone classiquement
permise entre lesquelles la particule effectue un mouvement périodique. Ces
points sont ceux où l'impulsion classique
limitant la zone classiquement
permise entre lesquelles la particule effectue un mouvement périodique. Ces
points sont ceux où l'impulsion classique
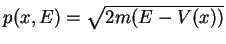 s'annule.
Les états liés quantiques correspondent aux valeurs de l'énergie où l'onde de
de Broglie
s'annule.
Les états liés quantiques correspondent aux valeurs de l'énergie où l'onde de
de Broglie
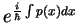 interfère de façon constructive
à chaque période:
interfère de façon constructive
à chaque période:
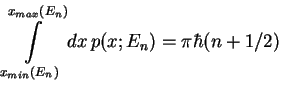 |
(7) |
Pour l'oscillateur harmonique, le membre de gauche vaut 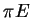 et on
retrouve exactement le résultat connu. Dans le cas anharmonique, montrer qu'on
doit avoir
et on
retrouve exactement le résultat connu. Dans le cas anharmonique, montrer qu'on
doit avoir
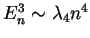 à suffisamment grand
à suffisamment grand 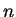 .
Cette expression possède-t-elle un développement en série entière autour de
.
Cette expression possède-t-elle un développement en série entière autour de
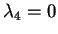 ?
?


Next: About this document ...
Up: td00
Previous: L'atome d'Hélium
Jean Orloff
2001-01-08
![]()
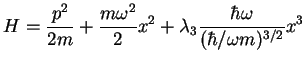
![$\displaystyle \Rightarrow E_{n}(\lambda _{3})=\hbar \omega [n+\frac{1}{2}+\frac{\lambda _{3}^{2}}{4}(-15n^{2}-15n-2)+O(\lambda _{3}^{4})],$](img288.gif)