- ... temps?1
- Réponse: formule de Rabi:
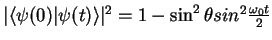
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... détectés2
- Les neutrinos interagissent très faiblement avec la matière: typiquement, un
neutrino de cette énergie traverse la terre entière sans être dévié. Les détecteurs
de neutrinos sont donc le plus gros possible.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....3
- Réponse:
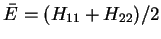 ;
;
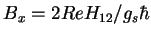 ;
;
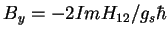 ;
;
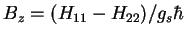 .
Cette possibilité d'introduire un spin fictif a pour origine la remarque suivante:
tout hamiltonien
.
Cette possibilité d'introduire un spin fictif a pour origine la remarque suivante:
tout hamiltonien 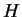 engendre au cours du temps une transformation unitaire
engendre au cours du temps une transformation unitaire
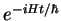 de l'espace des états. Pour un espace de dimension 2,
c'est donc une transformation de
de l'espace des états. Pour un espace de dimension 2,
c'est donc une transformation de 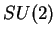 , le groupe des matrices unitaires
, le groupe des matrices unitaires
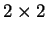 de déterminant 1, multipliée par une phase globale
de déterminant 1, multipliée par une phase globale 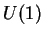 correspondant à
correspondant à 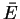 . Il se fait que l'algèbre infinitésimale du groupe
. Il se fait que l'algèbre infinitésimale du groupe
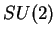 est la même que celle du groupe
est la même que celle du groupe 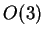 des rotations à 3 dimensions.
Ce spin fictif est cependant invariant sous l'action des rotations de l'espace
usuel, contrairement au vrai spin d'un électron.
des rotations à 3 dimensions.
Ce spin fictif est cependant invariant sous l'action des rotations de l'espace
usuel, contrairement au vrai spin d'un électron.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 4
- Dans le cas contraire, on peut toujours redéfinir
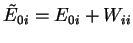 , et remplacer
, et remplacer 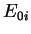 par
par
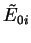 dans ce qui suit.
dans ce qui suit.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... associés.5
- Réponse:
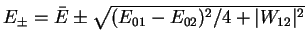 ;
;
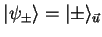 , avec
, avec
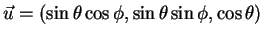 ,
et
,
et
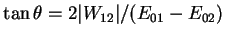 ;
;
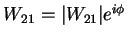 :
utiliser le résultat du 1.
:
utiliser le résultat du 1.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ....6
- Ceci n'est autre que le Wronskien
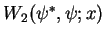 qui est constant
dans une solution stationnaire.
qui est constant
dans une solution stationnaire.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... potentiel:7
- Pour simplifier les notations, on pose
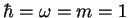 , ce qui revient
à mesurer resp.
, ce qui revient
à mesurer resp. 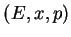 en unités de
en unités de
![$ (\hbar \omega ,[\hbar /\omega m]^{1/2},[\hbar \omega m]^{1/2}) $](img293.gif) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
l'une8
-
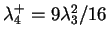
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... l'autre9
-
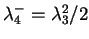
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
près.10
- On trouve
![$ E_{n}(\lambda _{3},\lambda _{4})=n+\frac{1}{2}+\frac{1}{4}\left[ (6\lambda _{4...
...{2})\right] +O(\lambda _{3}^{4},\lambda _{4}^{2},\lambda _{3}^{2}\lambda _{4}) $](img301.gif)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.