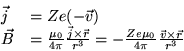
Soit un atome à 1 électron. Dans le référentiel où l'électron est au repos, le noyau crée un courant lors de sa rotation:
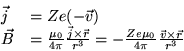
Comparé au champ électrostatique
![]() vu par l'électron, le champ magnétique est donc:
vu par l'électron, le champ magnétique est donc:
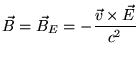
Ceci est cohérent avec la façon dont les champs électrique et magnétique se
mélangent sous une transformation de Lorentz. Sauf que la transformation de
Lorentz demande
![]() , et ici on est passé à un référentiel
tournant. Thomas a montré que cela induisait simplement un facteur
, et ici on est passé à un référentiel
tournant. Thomas a montré que cela induisait simplement un facteur
![]() dans le champ magnétique senti par l'électron. Comme celui-ci a un moment magnétique,
on a:
dans le champ magnétique senti par l'électron. Comme celui-ci a un moment magnétique,
on a:
où le facteur ![]() représente la précession de Thomas.
représente la précession de Thomas.
En utilisant le fait que
![]() et que
et que
![]() , on a:
, on a:
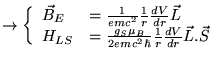
Or
![]() et
et
![]() , d'où:
, d'où:
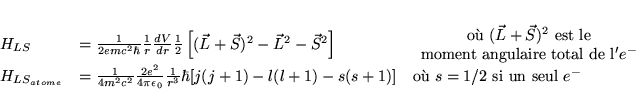
Cette dernière expression n'est valable que pour un atome de charge ![]() .
.
Seul
![]() est conservé par ce terme :
est conservé par ce terme :
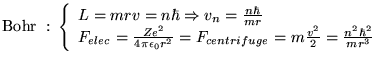
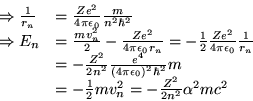
avec
![]() qui est la constante de structure fine.
qui est la constante de structure fine.

![\begin{displaymath}
\begin{array}{ll}
H_{LS} & \simeq \frac{1}{2m^{2}c^{2}}\frac...
...{n^{4}}\alpha ^{2}\frac{1}{2}[j(j+1)-l(l+1)-s(s+1)]
\end{array}\end{displaymath}](img428.gif)
Si
![]() alors
alors
![]() et on a:
et on a:
![$\displaystyle \Rightarrow \frac{1}{2}[j(j+1)-l(l+1)-s(s+1)]_{max}-\frac{1}{2}[j(j+1)-l(l+1)-s(s+1)]_{min}=l+\frac{1}{2}$](img433.gif)
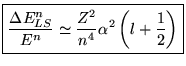
Si ![]() et
et ![]() : correspond à un champ magnétique extérieur
: correspond à un champ magnétique extérieur ![]() T
T![]() Gauss. Ceci donne l'ordre de grandeur du champ magnétique local que sent le
spin de l'électron.
Gauss. Ceci donne l'ordre de grandeur du champ magnétique local que sent le
spin de l'électron.
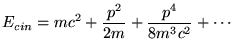
![]() : limite non-relativiste. Les termes suivant sont des
termes de correction: plus
: limite non-relativiste. Les termes suivant sont des
termes de correction: plus ![]() est proche de
est proche de ![]() plus il y en a.
plus il y en a.
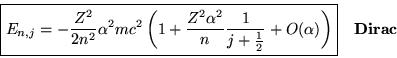
Cette équqtion ne dépend ni de ![]() ni de
ni de ![]() mais uniquement de
mais uniquement de ![]() .
.
Le proton a lui aussi un spin ![]() et une charge
et une charge ![]() qui a un moment
magnétique donné par:
qui a un moment
magnétique donné par:
avec
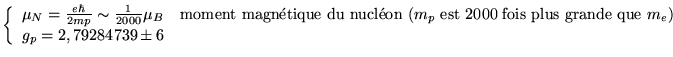
On s'attend à avoir pour le couplage entre le moment angulaire et le spin du proton:

C'est donc 2000 fois plus petit: correction ``hyper'' fine du niveau de l'énergie.
Il a lui aussi un spin ![]() . On peut donc écrire:
. On peut donc écrire:
Avec
![]()
Les nucléons sont constitués de deux types de quarks (Up et Down) dont voici
les charges:
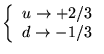 . Le proton est constitué de 2 quarks Up et d'un Down, donc sa charge totale
est bien égale à 1. Le neutron est constitué de 2 Down et 1 Up : sa charge est
bien nulle.
. Le proton est constitué de 2 quarks Up et d'un Down, donc sa charge totale
est bien égale à 1. Le neutron est constitué de 2 Down et 1 Up : sa charge est
bien nulle.
En fait, si
![]() le neutron pourrait être une particule élémentaire
neutre mais ce n'est pas le cas.
le neutron pourrait être une particule élémentaire
neutre mais ce n'est pas le cas.
Le spin du photon est égale à 1 (lié au caractère vectoriel du potentiel vecteur
![]() ). Si le spin est unitaire, on a alors 3 choix possibles
pour
). Si le spin est unitaire, on a alors 3 choix possibles
pour ![]() :
: ![]() .
.
Or ici, on a ![]() qui est interdit.
qui est interdit.