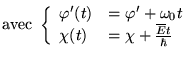


suivant: 1.12 Exemple: Couplage spin-orbite
monter: 1 Théorie générale des
précédent: 1.10 Exemple physique: moment
Table des matières
Sous-sections
On utilise l'appareil de Stern-Gerlach pour préparer le système dans un état
particulier (par exemple 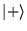 c'est-à-dire
c'est-à-dire  ).
).
Après mesure, on obtient:
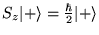 où
où
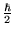 est la valeur mesurée avec
est la valeur mesurée avec  .
.
On privilégie une direction
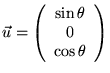 . On fait donc tourner le premier polariseur d'un angle
. On fait donc tourner le premier polariseur d'un angle 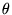 .
.
Où 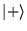 et
et 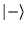 sont les vecteurs propres pour
sont les vecteurs propres pour
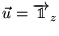
- Mesure dans un état parallèle à
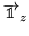 : le
deuxième analyseur est positionné dans l'axe des
: le
deuxième analyseur est positionné dans l'axe des 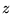 .
.
Dès que
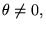 si
si 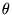 petit alors
petit alors
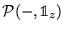 petite mais existe!
petite mais existe!
- Mesure dans un état parallèle à
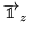 : le
deuxième analyseur est positionné dans l'axe des
: le
deuxième analyseur est positionné dans l'axe des 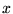 .
.
Remark
Tout hamiltonien
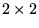
est de cette forme (à une composante
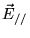
près):
Remark
Couplage fictif entre le moment magnétique de spin et le champ magnétique.
Theorem
Tout système à deux états peut se ramener à un spin (fictif) dans un champ magnétique
(fictif) une fois soustraite l'énergie moyenne
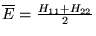
Les vecteurs propres sont:
Avec
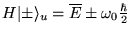 et
et
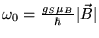 qui est la fréquence
de précession de Larmor.
qui est la fréquence
de précession de Larmor.
L'évolution temporelle du système est simple:
Par combinaison linéaire, on obtient pour un vecteur quelconque normalisé :
Remark
Un vecteur général s'écrit
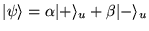
avec
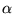
et
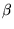
deux paramètres complexes. Si
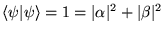
,
il reste 3 paramètres réels que l'on peut choisir comme
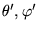
et
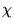
.
À un instant 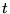 quelconque, on a:
quelconque, on a:
- Image géométrique
-
- Le vecteur
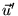 rprésentant l'état
rprésentant l'état
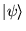 tourne autour
de l'axe
tourne autour
de l'axe
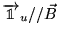 à la vitesse angulaire
à la vitesse angulaire
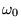 (précession de Larmor)
(précession de Larmor)
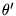 est constant, ainsi que
est constant, ainsi que
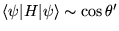 (conservation de l'énergie)
(conservation de l'énergie)
- La phase globale de
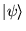 ,
, 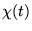 , progresse à la vitesse
angulaire
, progresse à la vitesse
angulaire
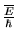 correspondant à l'énergie moyenne
des 2 états
correspondant à l'énergie moyenne
des 2 états
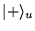 et
et
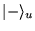 .
.



suivant: 1.12 Exemple: Couplage spin-orbite
monter: 1 Théorie générale des
précédent: 1.10 Exemple physique: moment
Table des matières
2000-10-19
![]() c'est-à-dire
c'est-à-dire ![]() ).
).
![]() où
où
![]() est la valeur mesurée avec
est la valeur mesurée avec ![]() .
.
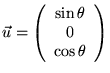 . On fait donc tourner le premier polariseur d'un angle
. On fait donc tourner le premier polariseur d'un angle ![]() .
.
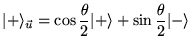
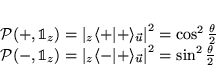
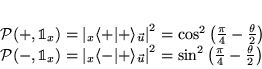
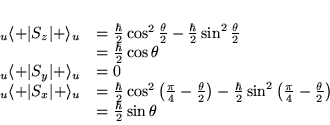
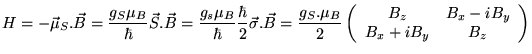
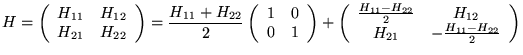
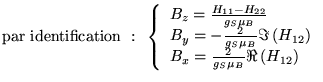
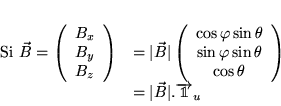
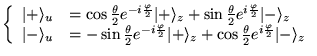
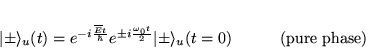
![% latex2html id marker 6430
$\displaystyle \vert\psi (t=0)\rangle =e^{-i\chi }\l...
... _{u}+\sin \frac{\theta '}{2}e^{i\frac{\varphi '}{2}}\vert-\rangle _{u}\right] $](img389.gif)
![% latex2html id marker 6446
$\displaystyle \vert\psi (t)\rangle =e^{-i\chi (t)}\...
...u}+\sin \frac{\theta '}{2}e^{i\frac{\varphi '(t)}{2}}\vert-\rangle _{u}\right] $](img397.gif)