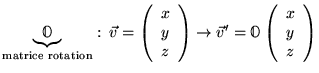
Application linéaire de
![]() respecte
le produit scalaire de
respecte
le produit scalaire de ![]() vecteurs, respecte les longueurs.
vecteurs, respecte les longueurs.
![]() : respect du produit scalaire (
: respect du produit scalaire (![]() ).
).
![]()
![]() groupe des matrices orthogonales.
groupe des matrices orthogonales.
![]()
![]() Groupe à
Groupe à ![]() paramètres continus :
paramètres continus :
Matrice orthogonale proche de la matrice unité :
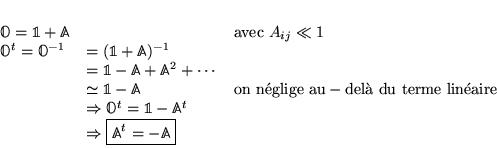
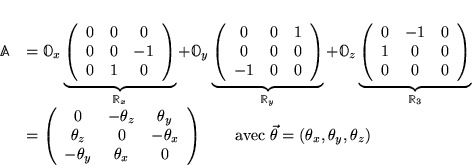
Sous l'action d'une rotation infinitésimale, l'action sur un vecteur à ![]() dimensions donne :
dimensions donne :
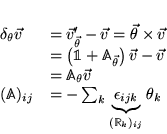
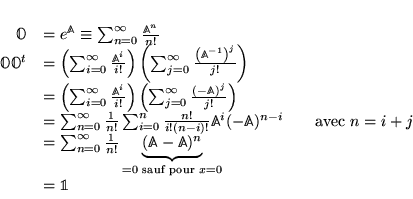
Si on exponentialise une matrice antisymétrique, alors la matrice que l'on obtient est orthogonale.
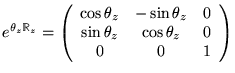 avec
avec
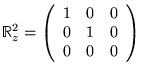 et
et
![]() où
où
![]() est
la matrice de rotation d'un angle
est
la matrice de rotation d'un angle ![]() autour de l'axe des
autour de l'axe des ![]() .
Le module du vecteur indique de combien on tourne, sa direction indique l'axe
de rotation.
.
Le module du vecteur indique de combien on tourne, sa direction indique l'axe
de rotation.
Soient ![]() rotations
rotations
![]() :
:
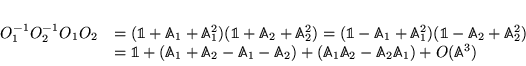
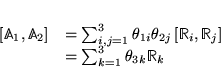
d'où :
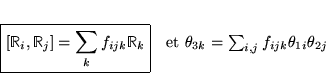
Où ![]() est une constante de structure.
est une constante de structure.
Ces commutations forment l'algèbre de Lie.
Des petites rotations contiennent entièrement la structure des grandes rotations grâce à l'exponentiation de ces petites rotations.
![% latex2html id marker 5516
$\displaystyle \displaystyle [\mathbb{R}_{i},\mathbb{R}_{j}]=\sum _{k=1}^{3}\epsilon _{ijk}\mathbb{R}_{k}$](img34.gif)
Soit ![]() telle que :
telle que :
![]() et
et
![]() tel que :
tel que :
![]() .
.
![]() car
car
![]()
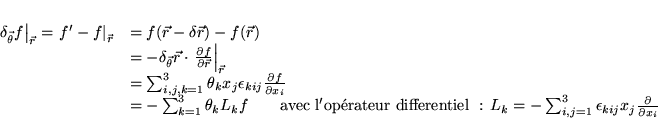
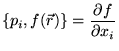
![]() avec
avec
![]() .
.
![]() est un moment angulaire. Donc
est un moment angulaire. Donc ![]() représente
le moment cinétique.
représente
le moment cinétique.
On s'intéresse maintenant plus particulièrement aux crochets de Poisson entre moments cinétiques :
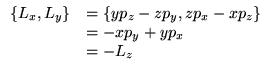
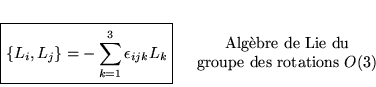
![]() est le générateur des rotations classiques.
est le générateur des rotations classiques.