On passe d'une grandeur ![]() à un opérateur :
à un opérateur :
![\begin{displaymath}
\begin{array}{rl}
L_{k} & \longrightarrow \hat{L}_{k}=\sum _...
...\right] =\sum _{k}i\hbar \epsilon _{ijk}\hat{L}_{k}
\end{array}\end{displaymath}](img52.gif)
![]() avec
avec
![]()
Quand on quantifie, on perd le moment cinétique, vecteur dont on connaît toutes
les composantes. On peut fixer ![]() et
et ![]() en même temps (crochets
de Poisson
en même temps (crochets
de Poisson
![]() commutateurs).
commutateurs).
On peut fixer une composante et la longueur du vecteur au mieux :
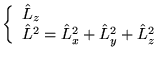
![$\displaystyle \left\{ \begin{array}{l}
\left[ \hat{L}_{z},\hat{L}_{\pm }\right]...
...{L}_{\pm }\right] =\left[ \hat{L}^{2},\hat{L}_{z}\right] =0
\end{array}\right. $](img63.gif)
![$ \begin{array}{ll}
\hat{L}^{2} & =\frac{1}{2}(L_{+}L_{-}+L_{-}L_{+})+L_{z}^{2}\...
...{-},L_{+}]+\hat{L}_{z}^{2}\\
& =L_{+}L_{-}-\hbar L_{z}+L_{z}^{2}
\end{array} $](img64.gif)