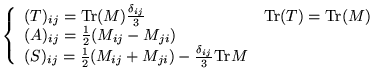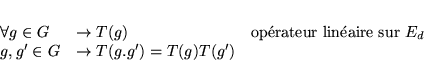
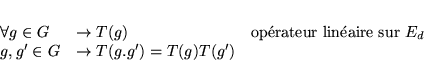
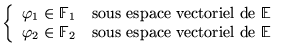

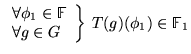

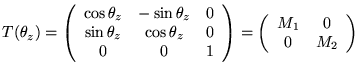
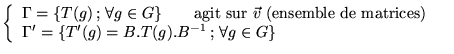
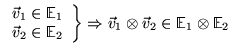
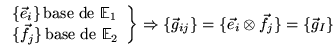 où
où
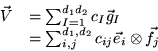
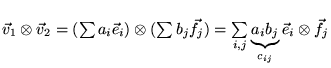
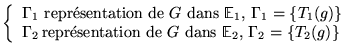 alors
alors
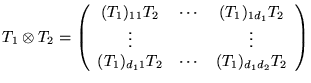
Si on prend
![]() on obtient
on obtient
![]() qui est l'espace des matrices
qui est l'espace des matrices
![]()
Au niveau de la représentation des matrices de rotation, on peut écrire
![]() où
où ![]() est une matrice symétrique sans trace :
est une matrice symétrique sans trace :
![]() ;
;
![]() est une matrice antisymétrique :
est une matrice antisymétrique :
![]() et
et ![]() la
trace de
la
trace de ![]() :
:
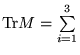 . En effet :
. En effet : ![]() avec :
avec :