



suivant: 2.5 Questions rapides
monter: 2 Espaces vectoriels de
précédent: 2.3 Norme
Table des matières
Armé d'une distance, on peut s'intéresser à la convergence d'une suite de fonctions
(ou de vecteurs). Il faut distinguer
- Convergence simple
- c'est la convergence de la fonction en chaque point
C'est une définition naturelle, mais insuffisante en analyse. En effet, on
ne peut permuter la limite
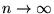 et les limites nécéssaires
au calcul infinitésimal. Exemples:
et les limites nécéssaires
au calcul infinitésimal. Exemples:
-
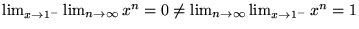
-
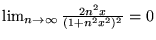 (fonction
nulle). Or
(fonction
nulle). Or
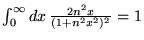
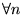 (en posant
(en posant 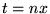 )
)
- Convergence uniforme (C.U.)
- par rapport au critère de convergence précédant,
on demande de plus que
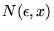 soit indépendant de
soit indépendant de 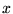 , ce
qui revient à demander que
, ce
qui revient à demander que
et donc que
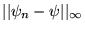 tende vers 0. C'est pourquoi
tende vers 0. C'est pourquoi
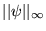 est parfois appelée norme de la convergence uniforme
est parfois appelée norme de la convergence uniforme
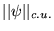 . La convergence uniforme permet d'échanger
. La convergence uniforme permet d'échanger 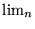 et
et
 et garantit que, par exemple, la limite d'une suite de dérivées
soit la dérivée de la limite. On peut vérifier en particulier que les problèmes
soulevés par la convergence simple dans les exemples précédants disparaissent:
dans ces cas, on n'avait pas convergence uniforme. La C.U. est un cas particulier
de
et garantit que, par exemple, la limite d'une suite de dérivées
soit la dérivée de la limite. On peut vérifier en particulier que les problèmes
soulevés par la convergence simple dans les exemples précédants disparaissent:
dans ces cas, on n'avait pas convergence uniforme. La C.U. est un cas particulier
de
- Convergence en norme
- qui a lieu pour une certaine norme si
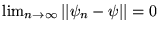 .
Si la convergence en norme implique convergence simple, le contraire n'est pas
vrai comme on l'a vu dans les 2 exemples.
.
Si la convergence en norme implique convergence simple, le contraire n'est pas
vrai comme on l'a vu dans les 2 exemples.




suivant: 2.5 Questions rapides
monter: 2 Espaces vectoriels de
précédent: 2.3 Norme
Table des matières
2000-10-06
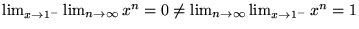
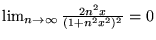 (fonction
nulle). Or
(fonction
nulle). Or
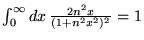
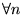 (en posant
(en posant 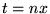 )
)
![$\displaystyle \psi _{1},\psi _{2},\ldots \psi _{n}\begin{array}[b]{c}
C.U.\\
\rightarrow
\end{array}\psi$](img235.gif)
![$\displaystyle \psi _{1},\psi _{2},\ldots \psi _{n}\begin{array}[b]{c}
C.U.\\
\rightarrow
\end{array}\psi$](img235.gif)