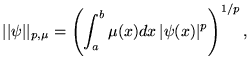On peut donc voir les fonctions comme des vecteurs dans un espace de dimension
généralement infinie. Une question qu'on peut se poser est de savoir si deux
points dans un tel espace sont proches l'un de l'autre ou non. Pour cela, on
a besoin du concept métrique de distance ou de norme
qui permet d'associer à tout vecteur 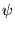 un réel positif
un réel positif 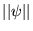 avec les propiétés suivantes:
avec les propiétés suivantes:
Remarque
Pour être précis, seule la dernière définition satisfait à la troisième condition
(
2.3.1) dans un espace de fonctions: en effet, la valeur d'une
intégrale ne change pas si l'on modifie l'intégrand en un point, ou en un ensemble
de mesure nulle de points. Pour que
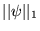
ou
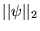
définissent des normes acceptables, il faut considérer toutes les fonctions
de norme nulle comme équivalentes; ceci revient à considérer un espace vectoriel
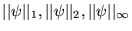
dont chaque point est une classe d'équivalence de fonctions
ne différant que par des fonctions de norme nulle. Dans des problèmes physiques,
ces subtilités sont sans effet car aucune mesure ne permet de distinguer entre
2 fonctions d'une même classe: la mécanique classique ne peut décrire l'infiniment
petit nécessaire à la définition d'un point mathématique, et en mécanique quantique,
le principe d'incertitude demande une impulsion (et donc une énergie) infiniment
grande pour sonder l'infiniment petit.
![]() un réel positif
un réel positif ![]() avec les propiétés suivantes:
avec les propiétés suivantes:
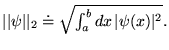 Les fonctions
pour lesquelles cette norme est finie forme l'espace vectoriel
Les fonctions
pour lesquelles cette norme est finie forme l'espace vectoriel