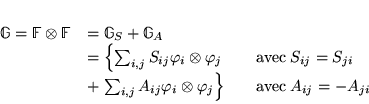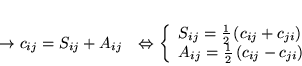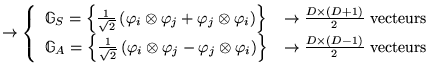Constatation naïve: les matrices ![]() forment un espace vectoriel
à
forment un espace vectoriel
à ![]() dimensions
dimensions
![]() .
.
Si
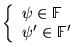 alors on peut définir
alors on peut définir ![]() tel que
tel que
![]()
On a par définition pour l'opération ![]() :
:
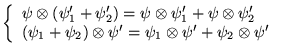
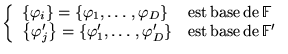 ,
,
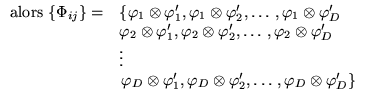
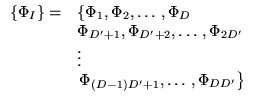 avec
avec
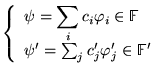
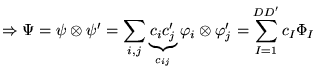 où les
où les ![]() sont les produits des
sont les produits des ![]() et des
et des ![]() .
.
Mais en général, on a une matrice
![]() de composantes
linéairement indépendantes.
de composantes
linéairement indépendantes.
Si
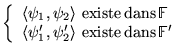
alors
![]() est
un bon produit scalaire dans
est
un bon produit scalaire dans
![]()
![]() :
:
![]()
![]() Si
Si
![]() alors
alors

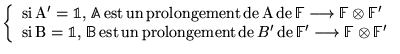 ,
,
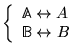 (par abus de notation)
(par abus de notation)
Si
![]()
alors
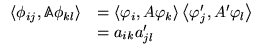
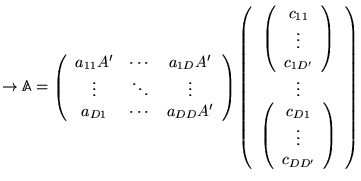 où
où ![]() est une matrice
est une matrice
![]() et les
et les ![]() sont des
vecteurs colonnes (
sont des
vecteurs colonnes (
![]() et
et
![]() )
)
![]() est une matrice de matrices.
est une matrice de matrices.
Si
![]() .
.
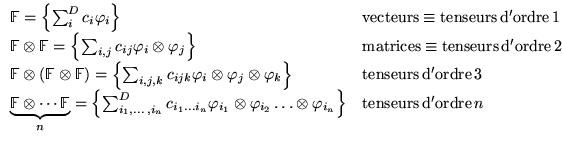
Sous un changement de base,
![]() , on a:
, on a:
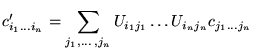 (linéarité,distributivité,
(linéarité,distributivité,![]() )
)
On peut décomposer l'espace de tenseurs d'ordre 2 en 2 sous-espaces: