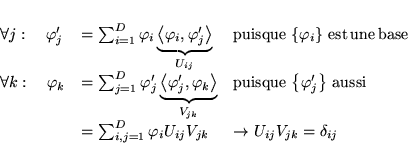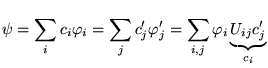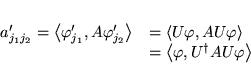suivant: 2.8 Produit tensoriel
monter: 2 Espaces vectoriels de
précédent: 2.6 Produit scalaire
Table des matières
Sous-sections
- Exemples:
Le produit est non-commutatif en général. (Cf Produit Mariciel)
Soit
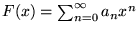 par définition du développement
de Taylor.
par définition du développement
de Taylor.
Exemple 2.7
Pour l'opérateur exponentiel.
Si 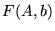 dépend d'un paramètre
dépend d'un paramètre 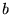 , on peut calculer l'opérateur
, on peut calculer l'opérateur
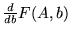
Exemple
Dérivation de l'opérateur exponentiel:
Exemple
Commutateur entre
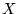
et
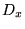
.
On définit pour tout
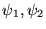 l'opérateur adjoint
l'opérateur adjoint
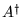 par rapport au produit scalaire
par rapport au produit scalaire
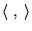 tel
que:
tel
que:
- Conséquences
-
Un opérateur hermitien est un opérateur qui vérifie
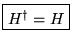
Exemple
L'opérateur impulsion.
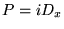 est hermitien sur
est hermitien sur  :
:
Remarque
Le caractère hermitien de l'opérateur dépend de

Ce sont les opérateurs qui vérifient:
- Conséquences
-
-
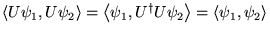
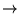 Conserve le produit scalaire et la norme (comme notations
dans
Conserve le produit scalaire et la norme (comme notations
dans
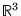 )
)
-
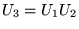 est unitaire
est unitaire
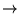 les opérateurs unitaires
forment un groupe sous le produit.
les opérateurs unitaires
forment un groupe sous le produit.
- Définitions
-
Théorème
Les valeurs propres
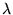
d'un opérateur hermitien
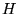
sont réelles.
Preuve.
Si
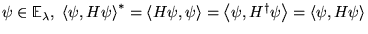
Or
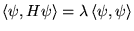
de plus
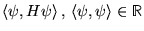
d'où
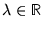

Théorème
Des vecteurs propres
associés à des valeurs propres
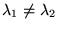
d'un opérateur hermitien
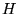
sont
orthogonaux:
Soit
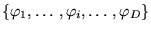 avec éventuellement
avec éventuellement 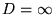 et
et
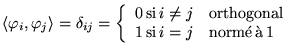
Théorème
Toute base dénombrable
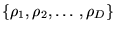
est orthonormalisable (Gram-Schmidt)
Preuve.
En effet, soient
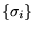
une base orthogonale, on
aura:

- Composantes
-
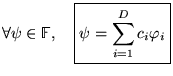 avec
avec
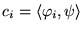
en effet
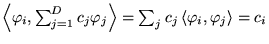
- Produit scalaire
-
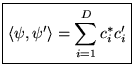
en effet
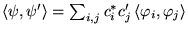
- Éléments de matrice d'un opérateur
- image des vecteurs de base.
Connaissant
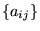 , on peut calculer l'image de tout
vecteur:
, on peut calculer l'image de tout
vecteur:
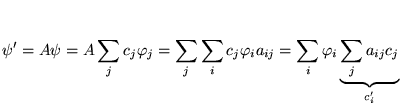
-
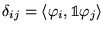 : ce
sont les éléments de matrice de l'opérateur identité
: ce
sont les éléments de matrice de l'opérateur identité
- Produit:
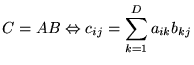 (produit matriciel)
(produit matriciel)
- Adjoint:
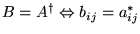
- Hermitien:
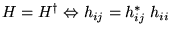 réels
réels
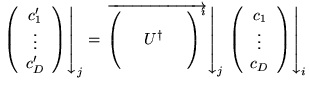
- Changement de base
- Soient
 bases orthonormées
bases orthonormées
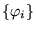 et
et
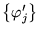 .
.
avec la convention d'Einstein (indice répété = somme sur cet indice), on a
donc:
De même
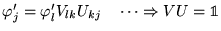
D'après ces deux équations, on peut dire que
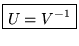
Or
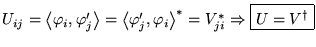
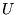 est donc une matrice unitaire (respecte les produits scalaires, en
particulier ceux des vecteurs de base)
est donc une matrice unitaire (respecte les produits scalaires, en
particulier ceux des vecteurs de base)
- Composantes:
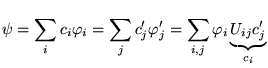
- Eléments de matrices:




suivant: 2.8 Produit tensoriel
monter: 2 Espaces vectoriels de
précédent: 2.6 Produit scalaire
Table des matières
2000-10-06
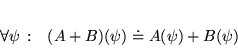
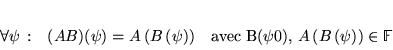
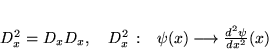
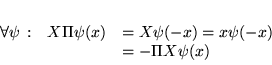
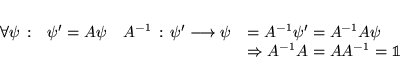
![]() il faudra restreindre
il faudra restreindre
![]() pour éliminer
pour éliminer
![]() si on veut inverser
si on veut inverser![]()
![]() par définition du développement
de Taylor.
par définition du développement
de Taylor.
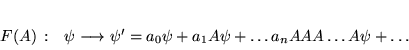
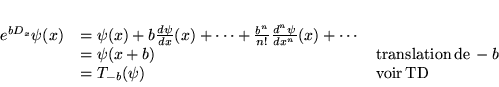
![]() dépend d'un paramètre
dépend d'un paramètre ![]() , on peut calculer l'opérateur
, on peut calculer l'opérateur
![]()
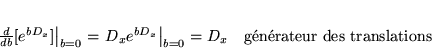
![\begin{displaymath}
% latex2html id marker 15450\begin{array}{rll}
\left[ X,D_...
...ll \psi \\
\left[ X,D_{x}\right] & =-\mathbb{1}&
\end{array}\end{displaymath}](img292.gif)
![]() l'opérateur adjoint
l'opérateur adjoint
![]() par rapport au produit scalaire
par rapport au produit scalaire
![]() tel
que:
tel
que:
![]()
![]() est hermitien sur
est hermitien sur ![]() :
:
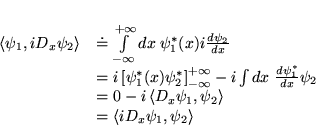

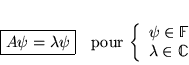
![]()
![]()
![]()
![]()
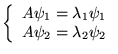
![]()
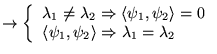
![]()
![]() avec éventuellement
avec éventuellement ![]() et
et
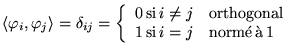
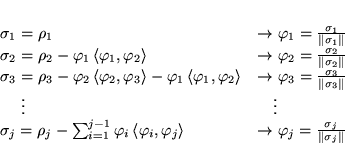
![]()
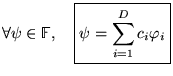 avec
avec
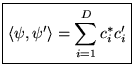
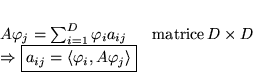
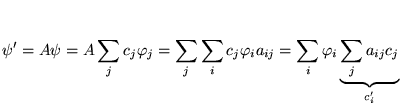
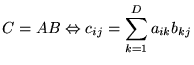 (produit matriciel)
(produit matriciel)