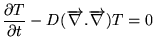suivant: 1.2 Résolution
monter: 1 Introduction: Refroidissement d'un
précédent: 1 Introduction: Refroidissement d'un
Table des matières
Sous-sections
En chaque point:
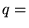 quantité
quantité- de chaleur/unité de volume
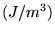
-
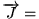 courant
courant
- de chaleur
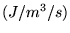
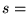 source
source- de chaleur
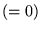
Il y a conservation car en l'absence de sources 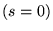 ,
, 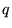 ne peut
changer qu'en créant un courant de chaleur. Le courant
ne peut
changer qu'en créant un courant de chaleur. Le courant
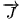 ``emporte'' la chaleur si
``emporte'' la chaleur si
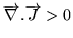 .
Dans un volume
.
Dans un volume 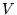 fixé, on a une variation de la chaleur totale:
fixé, on a une variation de la chaleur totale:
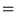 - (flux de
- (flux de
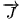 sortant), où
sortant), où 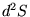 est
un élément de surface sur le bord de
est
un élément de surface sur le bord de 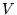 .
.
- Une variation de température entraîne une variation de la quantité
de chaleur :
si
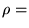 densité
densité
 et
et 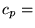 capacité calorifique
capacité calorifique
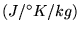
- Le flux de chaleur est induit par une différence spatiale de température
(Loi de Fourier):
- le signe ``
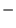 '' est dû au fait que le courant de chaleur va du plus
chaud au plus froid
'' est dû au fait que le courant de chaleur va du plus
chaud au plus froid
- le
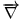 est dû au fait que le courant de chaleur
est proportionnel au gradient de température.
est dû au fait que le courant de chaleur
est proportionnel au gradient de température.
- la constante de proportionnalité
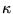 est la conductivité thermique
du matériau
est la conductivité thermique
du matériau
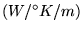 (
(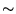 conductivité électrique pour
les métaux:
conductivité électrique pour
les métaux: 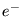 transportent à la fois électricité et chaleur...).
À titre indicatif,
transportent à la fois électricité et chaleur...).
À titre indicatif, 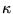 vaut 390 pour le cuivre et 0,025 pour
l'air
vaut 390 pour le cuivre et 0,025 pour
l'air
En insérant ces deux relations dans l'équation de conservation, on
arrive à l'équation de la chaleur
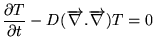 |
(1.1.1) |
à laquelle toute distribution de température physique
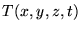 doit obéir. Dans cette équation,
doit obéir. Dans cette équation,
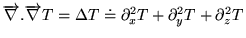 est le Laplacien scalaire, et
est le Laplacien scalaire, et 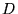 est le coefficient de diffusion
thermique
est le coefficient de diffusion
thermique 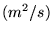 valant
valant
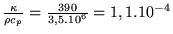 pour le cuivre et
pour le cuivre et
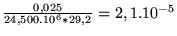 pour l'air.
Son interprétation microscopique est simple:
pour l'air.
Son interprétation microscopique est simple:
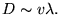 est
le produit de la vitesse moyenne
est
le produit de la vitesse moyenne 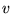 des particules transportant la chaleur
par leur libre parcours moyen
des particules transportant la chaleur
par leur libre parcours moyen 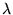 entre 2 collisions.
entre 2 collisions.




suivant: 1.2 Résolution
monter: 1 Introduction: Refroidissement d'un
précédent: 1 Introduction: Refroidissement d'un
Table des matières
2000-10-06
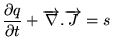
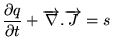
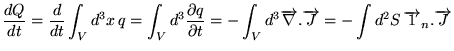
![]() - (flux de
- (flux de
![]() sortant), où
sortant), où ![]() est
un élément de surface sur le bord de
est
un élément de surface sur le bord de ![]() .
.