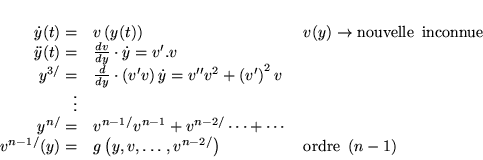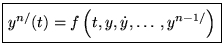 est un problème de Cauchy (C.I.)
est un problème de Cauchy (C.I.)
Si ![]() est continue en ses variables autour d'un point
est continue en ses variables autour d'un point
![]() alors
alors
![]() pour lequel une solution
pour lequel une solution ![]() existe
dans
existe
dans
![]() .
.
Si
![]() sont bornées,
sont bornées, ![]() est unique.
est unique.
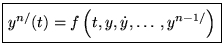 est un problème de Cauchy (C.I.)
est un problème de Cauchy (C.I.)
Si ![]() est continue en ses variables autour d'un point
est continue en ses variables autour d'un point
![]() alors
alors
![]() pour lequel une solution
pour lequel une solution ![]() existe
dans
existe
dans
![]() .
.
Si
![]() sont bornées,
sont bornées, ![]() est unique.
est unique.
Une famille à ![]() paramètres
paramètres
![]() est
une solution générale de l'équation différentielle d'ordre
est
une solution générale de l'équation différentielle d'ordre ![]()
![]() choix des CI de Cauchy
choix des CI de Cauchy
![]() il existe
des
il existe
des
![]() tels que
tels que
![]() soit solution.
soit solution.
![]() pour un choix particulier des paramètres
pour un choix particulier des paramètres
![]()