![]()
Cette équation différentielle linéaire est dite:
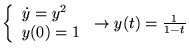
Si
![]() sont solutions d'une EDLH, alors
sont solutions d'une EDLH, alors
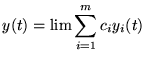 est aussi solution.
est aussi solution.
![]() on a un espace vectoriel de solutions équivalent à
on a un espace vectoriel de solutions équivalent à
![]()
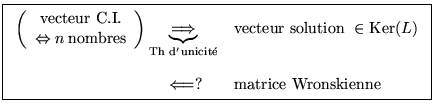
Si on a ![]() solutions
solutions
![]() on construit la
matrice carrée:
on construit la
matrice carrée:
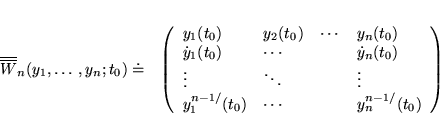
![]() Pour une combinaison linéaire arbitraire de cette base
Pour une combinaison linéaire arbitraire de cette base
![]() ,
on a:
,
on a:
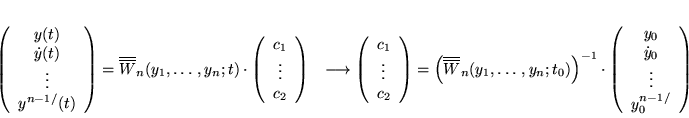
![]() On pourra trouver les
On pourra trouver les ![]() en fonction des C.I.
en
en fonction des C.I.
en ![]() si et seulement si
si et seulement si
![]() .
.
![]() Solution générale de l'équation diférentielle linéaire
homogène (SGEDLH) pour le problème de Cauchy.
Solution générale de l'équation diférentielle linéaire
homogène (SGEDLH) pour le problème de Cauchy.
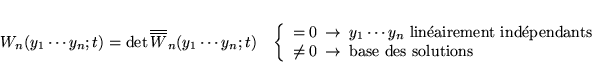
Si
![]() est une base des solutions de
est une base des solutions de ![]() ,
tout
,
tout ![]() est une combinaison linéaire des
est une combinaison linéaire des
![]() linéairement indépendants.
linéairement indépendants.
En fait:
![]() avec
avec
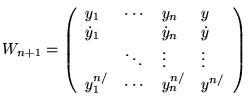
![]() est un opérateur différentiel linéaire et le coefficient de
est un opérateur différentiel linéaire et le coefficient de
![]() est
est ![]() : on calcule
: on calcule
![]() en fonction
des
en fonction
des
![]() donnés.
donnés.
Avantage:
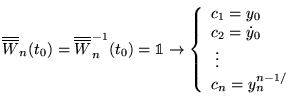
Pour un ensemble de ![]() solutions QCD,
solutions QCD,
![]()
![]()
![]() est donc
est donc
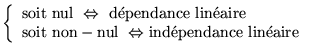
![]() , tant que
, tant que ![]() est intégrable.
est intégrable.
Contre-exemple:
![]() : singularité forte de EDL en
: singularité forte de EDL en
![]()
SGENH=SGEH+SPENH car la différence de deux SENH est solution de l'équation homogène. (SPENH=solution particulière de l'équation non-homogène)
Si on connaît la SGEH
![]()
![]() avec
avec
![]() (par exemple: le système fondamentale), on peut trouver une
SPENH de la forme:
(par exemple: le système fondamentale), on peut trouver une
SPENH de la forme:

![% latex2html id marker 17051
$ \rightarrow L[y]=c_{i}\overbrace{L[y_{i}]}^{=0}+R...
...R}_{1}\right) \, f_{n-2}+\left( R_{n}+R_{n-1}+\cdots R^{n-1/}_{1}\right) =g(t) $](img809.gif)
![]() On a une solution en prenant:
On a une solution en prenant:
![]() .
Mais on a:
.
Mais on a:
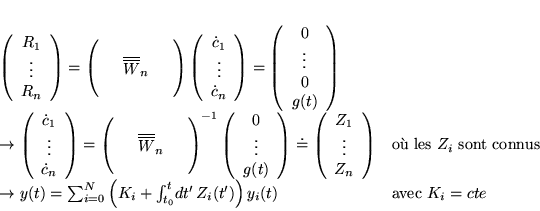
![]() est une SPENH.
est une SPENH.
On peut prendre par exemple
![]()
Comment trouver la SGEH?
Si on connaît une solution ![]() .
.
![]() on pose:
on pose:

![% latex2html id marker 17071
$ \rightarrow \, L[y]=z(t)\underbrace{L[y_{1}]}_{\equiv 0}+\dot{z}(\quad )+\cdots z^{n/}y_{1}=0 $](img815.gif)
![]() n'apparaît pas: on pose une nouvelle inconnue
n'apparaît pas: on pose une nouvelle inconnue ![]() ,
et on a une équation d'ordre
,
et on a une équation d'ordre ![]() en
en ![]()
![$ L[y]=\ddot{y}(t)+f_{1}(t)\dot{y}(t)+f_{2}(t)y(t)=z(t)\underbrace{L[y_{1}]}_{\equiv 0}+\dot{z}(t)(2\dot{y}_{1}+f_{1}y_{1})+\ddot{z}y_{1}=0 $](img820.gif)
![% latex2html id marker 17085
$ \begin{array}{l}
\displaystyle \rightarrow \frac{...
...)}\exp \int ^{t'}_{t_{0}}\! dt''\left[ -f_{1}(t'')\right] \right]
\end{array} $](img821.gif)
Tous les
![]() où
où
![]()
On pose
![]()
![]()
![]() équation caractéristique:
équation caractéristique: ![]() (polynôme de degré
(polynôme de degré
![]() )
)
il y a donc ![]() racines distinctes
racines distinctes
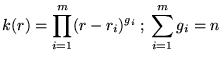
![$\displaystyle \displaystyle \rightarrow L[y]=\prod ^{m}_{i=1}\left( \frac{d}{dt}-r_{i}\right) ^{g_{i}}y(t)$](img829.gif)
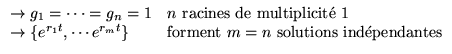
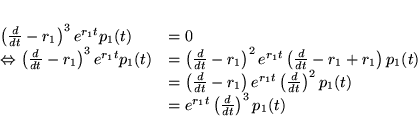
![]() appartient à un espace-vectoriel de dimension
appartient à un espace-vectoriel de dimension ![]() .
.