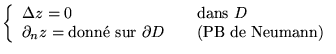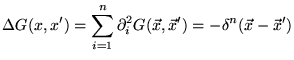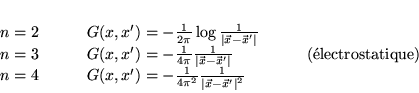Elles n'ont pas de caractéristiques réelles; pour ![]() ,
,
![]() .
.
On pose
![]() avec
avec
![]() .
.
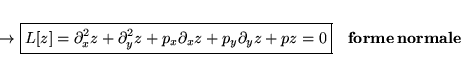
Supposons
![]() alors
alors
![]() (laplacien à
(laplacien à ![]() dimensions)
dimensions)
C'est-à-dire des C.I. sur ![]() qui n'est pas une courbe caractéristique.
Le problème de Cauchy est un problème mal posé (au sens d'Hadamard)
car instabilité par rapport aux C.I.
qui n'est pas une courbe caractéristique.
Le problème de Cauchy est un problème mal posé (au sens d'Hadamard)
car instabilité par rapport aux C.I.
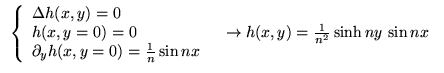
![]() croît sans limites à grand
croît sans limites à grand ![]()
![]() Si
Si ![]() est solution de
est solution de
![]() avec les C.I.
avec les C.I.
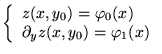
![]() est solution pour des C.I. à peine différentes (petit
est solution pour des C.I. à peine différentes (petit ![]() ).
).
Cette petite différence est exponentiellement amplifiée, et à une distance
![]() , elle devient d'ordre
, elle devient d'ordre ![]() !
!
C'est un problème bien posé. Exemple:
trouver
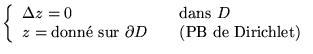 ou
ou