7.7 Équations paraboliques $\det p_{ij}=0\protect$

On les retrouve dans les équations de diffusion, de chaleur et d'options sur actions.

$n=2$: C'est le cas limite où les $2$ caractéristiques hyperboliques émanant d'un point se confondent avant de devenir imaginaires.

$\Leftrightarrow$ le coefficient de $\partial _{t}^{2}$ dans la forme normale hyperbolique s'annule; la caractéristique est $x=Cte$:

$$% latex2html id marker 18146\begin{array}{ll} \boxed{L[z]=... ...^{2}z-\partial _{t}z=0}& \textrm{EH la plus simple} \end{array}$$

$z$ peut d'interpréter comme une température: $L[z]=f(x,t)$ où $f$ représente la source de chaleur.

7.7.1 Conditions de Cauchy

On se donne $z(x,t=)=\varphi (x)$. Pour résoudre, on passe en transformée de Fourier:

$$% latex2html id marker 18158\begin{array}{l} z(x,t)=\int ^... ... }\frac{dk}{\sqrt{2\pi }}\tilde{\varphi }(k)e^{ikx} \end{array}$$

$L[z]=0$ $\Leftrightarrow -\partial _{t}\tilde{z}-k^{2}\tilde{z}=0$

$$% latex2html id marker 18164\begin{array}{lll} \displaysty... ...grale de Poisson }(\textrm{produit de convolution}) \end{array}$$

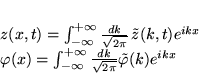
Solution bornée unique dans le demi-plan $t>0.$

7.7.2 Fonction de Green

$$G(x,t;x',t')=\left\{ \begin{array}{l... ...uad \textrm{pour }t>t'\\ 0 & \quad \textrm{pour }t\leq t' \end{array}\right.$$

$$L\left[ G(x,t)\right] =-\delta (x-x')\delta (t-t')$$

7.7.3 Problème mixte

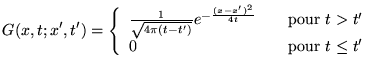
Il admet lui aussi une solution unique pour de C.L.:

$$% latex2html id marker 18176\begin{array}{ll} z(x=0,L;t)=\... ...quad \textrm{flux de chaleur fix}\acute{\textrm{e}} \end{array}$$

7.7.4 Problème au bord

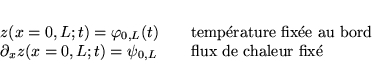
C'est un problème incompatible (Cf 7.5)