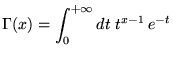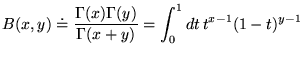suivant: 8.2 Équation et fonction
monter: 8 Quelques fonctions spéciales
précédent: 8 Quelques fonctions spéciales
Table des matières
Sous-sections
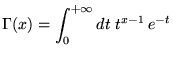 |
(8.1.1) |
Cette définition donne un nombre réel positif pour tout 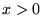 .
Elle reste aussi valable dans le demi-plan complexe
.
Elle reste aussi valable dans le demi-plan complexe
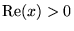 .
.
Figure 8.1.1:
Graphe de la fonction
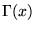 le long de l'axe
le long de l'axe  réel.
réel.
|
|
- Récurrence: (se démontre par parties)
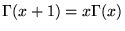 |
(8.1.2) |
Cette relation ne se déduit de (8.1.1) que pour
 ,
mais permet le prolongement analytique de
,
mais permet le prolongement analytique de
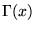 dans tout le plan
complexe, donnant des pôles en
dans tout le plan
complexe, donnant des pôles en 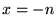 .
.
-
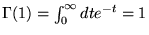
- Factorielle: pour
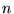 entier,
entier,
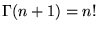 |
(8.1.3) |
-
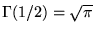 .8.1
.8.1
- Formule de Stirling: série asymptotique pour
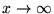 ,
,
![% latex2html id marker 18269
$\displaystyle \Gamma (x+1)\sim \sqrt{2\pi }x^{x+\frac{1}{2}}e^{-x}\, \left[ 1+\frac{1}{12x}+O(\frac{1}{x^{2}})\right]$](img1219.gif) |
(8.1.4) |
- Si
 est vu comme une généralisation de la factorielle,
on peut également généraliser les coefficients binomiaux:8.2
est vu comme une généralisation de la factorielle,
on peut également généraliser les coefficients binomiaux:8.2
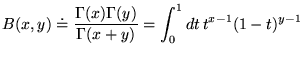 |
(8.1.5) |




suivant: 8.2 Équation et fonction
monter: 8 Quelques fonctions spéciales
précédent: 8 Quelques fonctions spéciales
Table des matières
2000-10-06