



suivant: 2.2 Espace vectoriel abstrait
monter: 2 Espaces vectoriels de
précédent: 2 Espaces vectoriels de
Table des matières
Sous-sections
2.1 Image naïve
On peut voir un vecteur usuel
de l'espace à 3 dimensions comme une application des indices 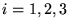 vers les réels, envoyant
vers les réels, envoyant
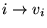
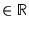 ,
, 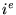 composante de
composante de
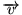 . Réciproquement, on peut aussi voir
une fonction
. Réciproquement, on peut aussi voir
une fonction
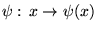 comme une sorte de vecteur
dont ``l'indice''
comme une sorte de vecteur
dont ``l'indice'' 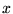 est continu:
est continu:
Cette image naïve soulève quelques problèmes, liés à la définition d'un ``index''
continu, et à la singularité de la ``base 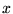 '' correspondante (c.f.
théorie des distributions). Néanmoins elle est très utile comme support à l'intuition,
à condition de savoir éviter les pièges. Pour cela, nous aurons besoin d'un
formalisme abstrait plus général et rigoureux.
'' correspondante (c.f.
théorie des distributions). Néanmoins elle est très utile comme support à l'intuition,
à condition de savoir éviter les pièges. Pour cela, nous aurons besoin d'un
formalisme abstrait plus général et rigoureux.
-
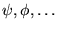 : fonctions des réels vers les complexes:
: fonctions des réels vers les complexes:
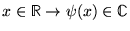 ;
;
-
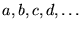 : nombres complexes;
: nombres complexes;
-
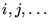 : indices variant de 1 à
: indices variant de 1 à 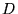 , dimension éventuellement
infinie;
, dimension éventuellement
infinie;
-
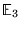 : dénotera l'espace vectoriel usuel des vecteurs
: dénotera l'espace vectoriel usuel des vecteurs 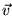 à 3 dimensions.
à 3 dimensions.
2000-10-06
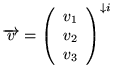
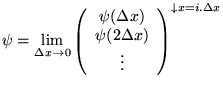
![]() '' correspondante (c.f.
théorie des distributions). Néanmoins elle est très utile comme support à l'intuition,
à condition de savoir éviter les pièges. Pour cela, nous aurons besoin d'un
formalisme abstrait plus général et rigoureux.
'' correspondante (c.f.
théorie des distributions). Néanmoins elle est très utile comme support à l'intuition,
à condition de savoir éviter les pièges. Pour cela, nous aurons besoin d'un
formalisme abstrait plus général et rigoureux.