



suivant: 2.3 Norme
monter: 2 Espaces vectoriels de
précédent: 2.1 Image naïve
Table des matières
Pour définir un espace vectoriel
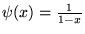 , il faut avoir:
, il faut avoir:
- l' addition
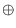 des vecteurs. C'est une loi de groupe commutatif
permettant de faire la somme de deux vecteurs.
des vecteurs. C'est une loi de groupe commutatif
permettant de faire la somme de deux vecteurs.
- pour les vecteurs usuels de l'espace euclidien à 3 dimensions
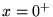 ,
le nouveau vecteur
,
le nouveau vecteur
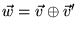 s'obtient en additionant
chaque composante séparément:
s'obtient en additionant
chaque composante séparément:
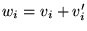 . Les propriétés voulues
de
. Les propriétés voulues
de 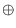 découlent du groupe commutatif de l'addition sur les composantes
réelles, de sorte qu'il n'est pas nécessaire de les distinguer:
découlent du groupe commutatif de l'addition sur les composantes
réelles, de sorte qu'il n'est pas nécessaire de les distinguer:
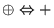 .
.
- pour les fonctions,
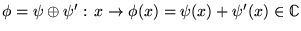 est de même défini comme une addition en chaque point séparément; par le même
abus de notation on la notera
est de même défini comme une addition en chaque point séparément; par le même
abus de notation on la notera 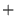 tout simplement.
tout simplement.
- des scalaires
-
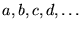 formant un corps. Ce sera le corps des
nombres complexes
formant un corps. Ce sera le corps des
nombres complexes
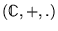 . Pour rappel, un corps est une structure
avec 2 lois de groupe commutatif
. Pour rappel, un corps est une structure
avec 2 lois de groupe commutatif 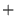 et
et  avec distributivité de
l'une sur l'autre.
avec distributivité de
l'une sur l'autre.
- la multiplication
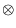 d'un vecteur par un scalaire. Celle-ci permet
de construire un nouveau vecteur
d'un vecteur par un scalaire. Celle-ci permet
de construire un nouveau vecteur
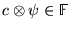 à partir
de n'importe quel vecteur
à partir
de n'importe quel vecteur 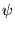 et scalaire
et scalaire 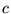 , avec les propriétés:
, avec les propriétés:
- Vecteurs usuels:
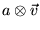 s'obtient en multipliant chaque composante
par
s'obtient en multipliant chaque composante
par 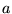 . À nouveau, ces propriétés découlent de la multiplication dans
. À nouveau, ces propriétés découlent de la multiplication dans
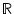 , et on peut simplifier les notations en prenant
, et on peut simplifier les notations en prenant
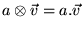 ,
ou tout simplement
,
ou tout simplement 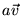 .
.
- Fonctions:
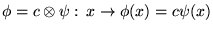 multipliant
la fonction par un même nombre en chaque point définit bien une telle multiplication
scalaire. On notera le nouveau vecteur tout simplement
multipliant
la fonction par un même nombre en chaque point définit bien une telle multiplication
scalaire. On notera le nouveau vecteur tout simplement 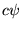 pour abréger.
pour abréger.
Dès qu'on a un espace vectoriel de dimension 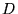 ,
on peut tenter de trouver une base, c'est-à-dire un ensemble
de vecteurs
,
on peut tenter de trouver une base, c'est-à-dire un ensemble
de vecteurs
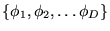 possédant les propriétés:
possédant les propriétés:
Comme exemple, on pourrait prendre l'ensemble des monômes
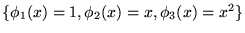 qui forme bien une base de l'espace vectoriel
qui forme bien une base de l'espace vectoriel
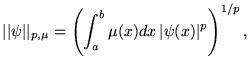 des polynômes
du second degré.
des polynômes
du second degré.
On peut démontrer que tout espace vectoriel de dimension finie 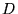 possède
au moins une base, et est donc isomorphe à
possède
au moins une base, et est donc isomorphe à 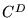 , l'espace des
, l'espace des 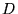 -tuplets
de nombres
-tuplets
de nombres
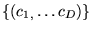 ; les espaces de même dimension sont
donc isomorphes entre eux. Par contre, les espaces de fonctions sont en général
infinis et doivent être distingués. Par exemple, l'espace
; les espaces de même dimension sont
donc isomorphes entre eux. Par contre, les espaces de fonctions sont en général
infinis et doivent être distingués. Par exemple, l'espace
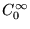 des séries de Taylor autour de
des séries de Taylor autour de 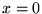 est différent de
est différent de
![$ C_{[0,2]}^{0} $](img191.gif) ,
espace des fonctions continues sur l'intervalle
,
espace des fonctions continues sur l'intervalle ![$ [0,2] $](img192.gif) : en effet,
: en effet,
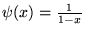 possède un développement de Taylor sans être continue. À l'inverse,
possède un développement de Taylor sans être continue. À l'inverse,
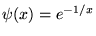 est continue sur l'intervalle donné, mais ne peut se représenter par son développement
de Taylor autour de
est continue sur l'intervalle donné, mais ne peut se représenter par son développement
de Taylor autour de 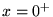 , puisque les coefficients en sont tous nuls
(ou infinis si l'on prend
, puisque les coefficients en sont tous nuls
(ou infinis si l'on prend 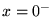 : c'est une singularité essentielle).
: c'est une singularité essentielle).




suivant: 2.3 Norme
monter: 2 Espaces vectoriels de
précédent: 2.1 Image naïve
Table des matières
2000-10-06
![]() , il faut avoir:
, il faut avoir:
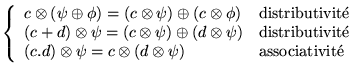
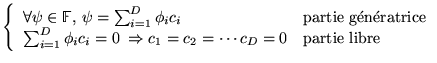
![]() possède
au moins une base, et est donc isomorphe à
possède
au moins une base, et est donc isomorphe à ![]() , l'espace des
, l'espace des ![]() -tuplets
de nombres
-tuplets
de nombres
![]() ; les espaces de même dimension sont
donc isomorphes entre eux. Par contre, les espaces de fonctions sont en général
infinis et doivent être distingués. Par exemple, l'espace
; les espaces de même dimension sont
donc isomorphes entre eux. Par contre, les espaces de fonctions sont en général
infinis et doivent être distingués. Par exemple, l'espace
![]() des séries de Taylor autour de
des séries de Taylor autour de ![]() est différent de
est différent de
![]() ,
espace des fonctions continues sur l'intervalle
,
espace des fonctions continues sur l'intervalle ![]() : en effet,
: en effet,
![]() possède un développement de Taylor sans être continue. À l'inverse,
possède un développement de Taylor sans être continue. À l'inverse,
![]() est continue sur l'intervalle donné, mais ne peut se représenter par son développement
de Taylor autour de
est continue sur l'intervalle donné, mais ne peut se représenter par son développement
de Taylor autour de ![]() , puisque les coefficients en sont tous nuls
(ou infinis si l'on prend
, puisque les coefficients en sont tous nuls
(ou infinis si l'on prend ![]() : c'est une singularité essentielle).
: c'est une singularité essentielle).