Oscillateur Anharmonique

On considère le degré de liberté de vibration d'une molécule diatomique polaire, c'est-à-dire la distance $R$ entre les deux noyaux. Le potentiel liant ces noyaux possède un minimum pour une certaine valeur $R_{0}$ de la distance (typiquement de l'ordre de quelques angstroms), et on peut tenter un développement en série de Taylor autour de ce minimum: $V(R)=V_{0}+k(R-R_{0})^{2}/2+k_{3}(R-R_{0})^{3}+\ldots$ Physiquement, on s'attend à ce que $V(R\rightarrow 0)\sim \frac{1}{R}$ et $V(R\rightarrow \infty )\sim Cte$, de sorte que la symétrie de réflexion autour de $R_{0}$ est brisée et n'interdit pas $k_{3}\not =0$; on s'attendrait plutôt à $k_{3}<0$.

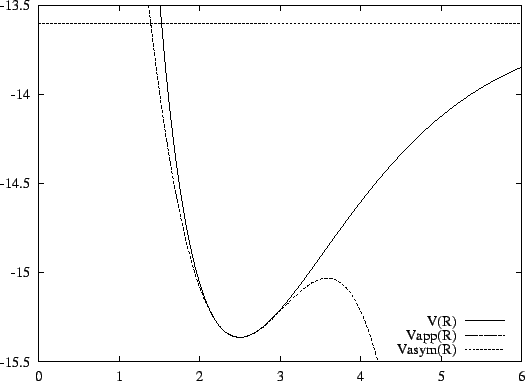
Pour étudier les effets d'un tel terme anharmonique, on va utiliser la théorie de perturbation autour de $k_{3}=0$.Définissant $x=(R-R_{0})$, on a

$$H = \frac{p^{2}}{2m}+V_{0}+\frac{k}{2}x^{2}+k_{3} x^{3}$$

$$= H_{0}+\lambda \hbar \omega \left( \frac{x}{a_{0}}\right) ^{3}$$

où $\lambda$ est une constante, proportionnelle et équivalente à $k_{3}$ et $H_{0}=V_{0}+p^{2}/2m+m\omega ^{2}x^{2}/2=V_{0}+\hbar \omega (a^{\dagger }a+1/2)$ est l'Hamiltonien connu de l'oscillateur harmonique, dont les états propres orthonormés $\vert\phi _{n}\rangle =a^{\dagger }\vert\phi _{n-1}\rangle /\sqrt{n}=a^{\dagger ^{n}}\vert\phi _{0}\rangle /\sqrt{n!}$ correspondent aux énergies $E_{n}=V_{0}+\hbar \omega (n+1/2)$. La pulsation fondamentale est $\omega =\sqrt{k/m}$ et la taille caractéristique des états quantiques est $a_{0}=\sqrt{\hbar /m\omega }$. L'opérateur d'annihilation, $a=(x/a_{0}+ipa_{0}/\hbar )/\sqrt{2}$, obéit aux relations canoniques $[a,a^{\dagger }]=1$. La perturbation dont on veut étudier l'effet est donc

$$W=\hbar \omega (x/a_{0})^{3}=\frac{\hbar \omega }{2^{3/2}}(a+a^{\dagger })^{3}$$

Éléments de matrices de $W\protect$

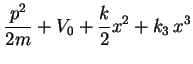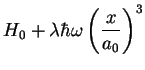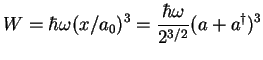
Calculer tous les éléments de matrice non-nuls de la perturbation entre des états non-perturbés.

Déplacement des niveaux

En déduire les déplacements des niveaux d'énergie au premier et au deuxième ordre en $\lambda$. Donner en particulier l'écart entre 2 niveau successifs $E_{n}(\lambda )-E_{n-1}(\lambda )$. Montrer que cet écart devient négatif pour $n>2/15\lambda ^{2}$. Par conséquent $E_{n}(\lambda )$ diminue sans limite pour grand $n$ et la théorie de perturbations introduit des dégénerescences absentes du problème non perturbé: peut-on dès lors en croire les résultats? Pour voir si la théorie de perturbation est seule en cause, cherchez une interprétation de ce résultat en étudiant le graphe de la fonction $V(x)=V_{0}+\hbar \omega [(x/a_{0})^{2}/2+\lambda (x/a_{0})^{3}]$, et en se rappelant que dans un état non perturbé, $\langle x^{2}\rangle _{n}=(n+1/2)a_{0}^{2}$. Si un traitement exact de ce potentiel était possible, donnerait-il le même genre de résultats? L'inclusion d'un terme positif en $x^{4}$ changerait-il ce problème?

États propres

Donner les états propres au premier ordre de la théorie de perturbations. Montrer que les éléments de matrices de l'opérateur $x$ $\langle \psi _{2}\vert x\vert\psi _{0}\rangle \sim \langle \psi _{4}\vert x\vert\psi _{0}\rangle \sim \lambda$ alors que ces éléments de matrices sont nuls entre les états non-perturbés correspondant.

Moment dipolaire électrique et spectre d'émission

Le dipôle électrique d'une molécule polaire est en première approximation $D=qR=qR_{0}+qx$ (avec $q$ une charge effective reflétant la séparation partielle de charge sur la distance $R$). Montrer qu'en l'absence de perturbation ( $\lambda =0$), la valeur moyenne de ce dipôle dans un état arbitraire $\vert\psi \rangle =\sum _{n}c_{n}\vert\phi _{n}\rangle$ sera une fonction oscillante du temps, de pulsation $\omega$; dans cet état, le dipôle émettra donc une onde électromagnétique monochromatique de longueur d'onde $c/\omega$.

Si par contre on tient compte de la perturbation au premier ordre ( $1\gg \lambda \not =0$), montrer qu'un état arbritraire $\vert\psi \rangle =\sum _{n}d_{n}\vert\psi _{n}\rangle$ émettra non-seulement une série de longueurs d'ondes proches de $c/\omega$, mais émettra aussi avec une intensité plus faible des longueurs d'ondes proches de $c/2\omega$ et de $c/4\omega$. Suggérer deux manières d'estimer $\lambda$ à partir du spectre de fréquence.