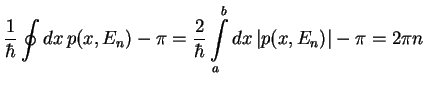

Next: Système à 2 états:
Up: td00
Previous: Oscillateur Anharmonique
Dans un potentiel 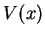 constant à une dimension, l'énergie cinétique
classique est constante et l'impulsion aussi. L'équation de Schroedinger
constant à une dimension, l'énergie cinétique
classique est constante et l'impulsion aussi. L'équation de Schroedinger
![$\displaystyle i\hbar \partial _{t}\psi (x,t)=H\psi (x,t)=[-\hbar ^{2}\partial ^{2}_{x}\psi /2m+V(x)]\psi (x,t)$](img187.gif)
admet des solutions stationnaires qui sont alors simplement des ondes planes:
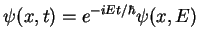
avec
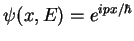 et
et
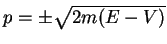 . Si
. Si  varie très lentement tout en restant inférieur à
varie très lentement tout en restant inférieur à  , on s'attend à pouvoir
remplacer dans
, on s'attend à pouvoir
remplacer dans
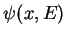 la constante
la constante 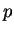 par la valeur locale
de l'impulsion classique au point
par la valeur locale
de l'impulsion classique au point 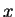 considéré:
considéré:
![$ p\rightarrow p(x,E)=\pm \sqrt{2m[E-V(x)]} $](img194.gif) .
Ceci donne une fonction d'onde semi-classique, dans la mesure où on se donne
à la fois la position et l'impulsion classique.
.
Ceci donne une fonction d'onde semi-classique, dans la mesure où on se donne
à la fois la position et l'impulsion classique.
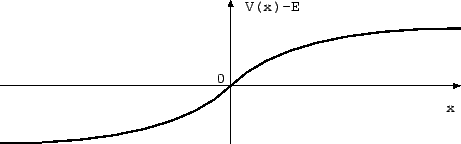
- Cette fonction d'onde viole-t-elle le principe d'incertitude?
- Montrer que l'expression correcte est en fait
Pour cela, poser
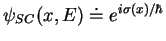 , insérer
cette forme dans l'équation de Schroedinger et développer
, insérer
cette forme dans l'équation de Schroedinger et développer
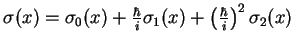 en puissances de
en puissances de 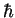 . Montrer que le préfacteur
. Montrer que le préfacteur
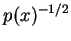 est nécessaire à une interprétation correcte du courant de probabilité
est nécessaire à une interprétation correcte du courant de probabilité
![$ j_{x}(x,t)=\frac{\hbar }{m}Im[\psi ^{*}(x,t)\partial _{x}\psi (x,t)] $](img200.gif) .6 Pour rappel, ce courant intervient dans l'équation de continuité:
.6 Pour rappel, ce courant intervient dans l'équation de continuité:
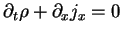 qui exprime la conservation de la densité de probabilité
qui exprime la conservation de la densité de probabilité
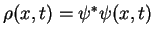 .
.
- Quelle est la limite de validité de ce développement en
 ? Le développement
de
? Le développement
de
 correspond-il à un développement de Taylor usuel? Dans
la suite, on posera par un choix de dimensions
correspond-il à un développement de Taylor usuel? Dans
la suite, on posera par un choix de dimensions 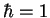 pour simplifier
les notations.
pour simplifier
les notations.
- Dans une région classiquement interdite,
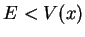 , on peut sous les mêmes
conditions obtenir 2 solutions approchées
, on peut sous les mêmes
conditions obtenir 2 solutions approchées
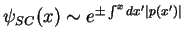 .
Quel phénomène bien connu ces fonctions d'onde décrivent-elles? Si la région
interdite s'étend jusque
.
Quel phénomène bien connu ces fonctions d'onde décrivent-elles? Si la région
interdite s'étend jusque 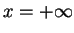 , une des deux solutions est interdite:
laquelle? Que vaut dans ce cas le courant de probabilité? Interpréter physiquement
ce résultat.
, une des deux solutions est interdite:
laquelle? Que vaut dans ce cas le courant de probabilité? Interpréter physiquement
ce résultat.
- En un point de rebroussement (prenons par exemple
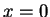 ), l'impulsion
classique s'annule: l'approximation semi-classique est-elle valable? On peut
néanmoins tenter de raccorder les comportements trouvés de part et d'autre en
continuant la fonction
), l'impulsion
classique s'annule: l'approximation semi-classique est-elle valable? On peut
néanmoins tenter de raccorder les comportements trouvés de part et d'autre en
continuant la fonction  et les solutions asymptotiques
et les solutions asymptotiques
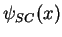 dans le plan complexe
dans le plan complexe
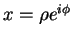 , de façon à éviter
, de façon à éviter 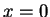 .
.
On s'attend donc à trouver pour une fonction qui serait décroissante à droite
En particulier, on voit que le déphasage de 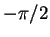 entre l'onde incidente
entre l'onde incidente
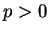 et l'onde réfléchie
et l'onde réfléchie 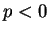 provient du préfacteur
provient du préfacteur 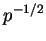 .
Le facteur
.
Le facteur  et la raison pour laquelle on ne peut faire le même raisonnement
pour ``recoller'' les fonctions avec
et la raison pour laquelle on ne peut faire le même raisonnement
pour ``recoller'' les fonctions avec
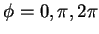 au lieu des
valeurs choisies ici ne peuvent se comprendre que par le phénomène de Stokes
dans la théorie des séries asymptotiques.
au lieu des
valeurs choisies ici ne peuvent se comprendre que par le phénomène de Stokes
dans la théorie des séries asymptotiques.
- Règle de quantification de Bohr-Sommerfeld: si on a un potentiel pour
lequel la région classiquement permise est d'extension finie, comprise entre
2 points de rebroussements
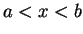 , la trajectoire classique pour une énergie
, la trajectoire classique pour une énergie
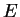 donnée est une courbe fermée dans l'espace des phases
donnée est une courbe fermée dans l'espace des phases 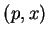 .
On peut alors répéter l'argument précédant au voisinnage de chaque point de
rebroussement. Une onde partant de
.
On peut alors répéter l'argument précédant au voisinnage de chaque point de
rebroussement. Une onde partant de 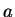 verra sa phase augmenter de
verra sa phase augmenter de
 pour atteindre
pour atteindre  puis de
puis de 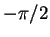 en se réfléchissant de
en se réfléchissant de 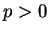 à
à 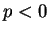 . Pour revenir en
. Pour revenir en 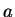 , la phase augmente ensuite de
, la phase augmente ensuite de
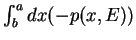 ,
qui a la même valeur que la première intégrale. En
,
qui a la même valeur que la première intégrale. En 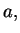 l'onde se réflechit,
avec un nouveau changement de phase de
l'onde se réflechit,
avec un nouveau changement de phase de 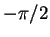 , et le cycle recommence.
Chaque cycle contribue à la fonction d'onde totale et pour qu'il interfère constructivement
avec les précédants, il faut un déphasage de
, et le cycle recommence.
Chaque cycle contribue à la fonction d'onde totale et pour qu'il interfère constructivement
avec les précédants, il faut un déphasage de 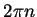 entre 2 passages
successifs, soit (dans des unités non-fondamentales où
entre 2 passages
successifs, soit (dans des unités non-fondamentales où
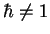 )
ce qui n'est possible que pour des valeurs discrètes de l'énergie
)
ce qui n'est possible que pour des valeurs discrètes de l'énergie 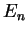 .
Interpréter géométriquement l'intégrale
.
Interpréter géométriquement l'intégrale
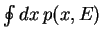 dans l'espace
des phases classique
dans l'espace
des phases classique 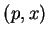 et faire le lien avec la mécanique statistique
où le nombre d'états quantiques est proportionnel au volume dans l'espace des
phases. Le résultat semi-classique est à priori valable pour
et faire le lien avec la mécanique statistique
où le nombre d'états quantiques est proportionnel au volume dans l'espace des
phases. Le résultat semi-classique est à priori valable pour 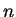 grand;
montrer que pour
grand;
montrer que pour 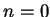 , grâce au déphasage de réflection, le résultat obtenu
n'est pas en contradiction avec le principe d'incertitude.
, grâce au déphasage de réflection, le résultat obtenu
n'est pas en contradiction avec le principe d'incertitude.
- Dans le cas de l'oscillateur harmonique: tracer les courbes
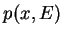 dans l'espace des phases, calculer les niveaux d'énergie prévus par cet argument
semi-classique et comparer la fonction d'onde
dans l'espace des phases, calculer les niveaux d'énergie prévus par cet argument
semi-classique et comparer la fonction d'onde
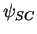 avec le résultat
exact connu.
avec le résultat
exact connu.


Next: Système à 2 états:
Up: td00
Previous: Oscillateur Anharmonique
Jean Orloff
2001-01-08
![]() constant à une dimension, l'énergie cinétique
classique est constante et l'impulsion aussi. L'équation de Schroedinger
constant à une dimension, l'énergie cinétique
classique est constante et l'impulsion aussi. L'équation de Schroedinger

![$\displaystyle \psi _{SC}(x,E)=\frac{1}{\sqrt{p(x,E)}}e^{\frac{i}{\hbar }\int ^{x}dx'p(x',E)}\: [1+O(\hbar )]$](img196.gif)
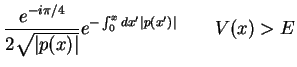
![$\displaystyle \frac{e^{-i\pi /4}}{\sqrt{\vert p(x)\vert}}\left[ e^{+i\pi /4+i\i...
... p(x')\vert}+e^{-i\pi /4-i\int _{0}^{x}dx'\vert p(x')\vert}\right] \quad V(x)<E$](img231.gif)