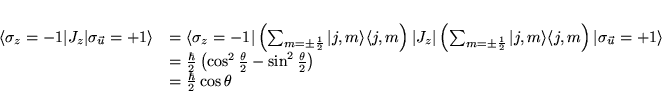![]() : moment angulaire demi-entier. Si
: moment angulaire demi-entier. Si ![]()
![]() : il y a deux états possibles.
: il y a deux états possibles.
![]()

![]()
En général, on a des fonctions arbitraires :
![]()
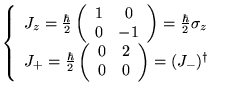
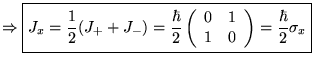
On voit que
![]() et :
et :
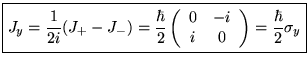
![]() : matrices de Pauli :
base de matrices hermitiennes
: matrices de Pauli :
base de matrices hermitiennes ![]() de trace nulle.
de trace nulle.
On a les propriétés suivantes :
![$\displaystyle \left\{ \begin{array}{l}
\sigma _{i}=\sigma _{i}^{\dagger }\\
\...
..._{j}\sigma _{i}=2\delta _{ij}=[\sigma _{i},\sigma _{j}]_{+}
\end{array}\right. $](img194.gif)
Quelle est l'action de ces rotations sur les représentations
![]() ?
?
En effet, si
![]()
![]() .
Ainsi on a les bonnes relations de commutation pour
.
Ainsi on a les bonnes relations de commutation pour ![]() On obtient
:
On obtient
:
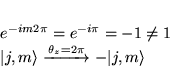
Soit
![]() cette direction. On a alors :
cette direction. On a alors :
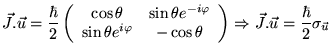
Où
![]() est un opérateur. On peut montrer que :
est un opérateur. On peut montrer que :
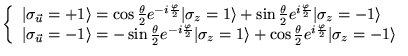
![$\displaystyle \left\{ \begin{array}{l}
\vert\sigma _{x}=\pm 1\rangle =\frac{1}{...
...gma _{z}=+1\rangle \pm i\vert\sigma _{z}=-1\rangle \right]
\end{array}\right. $](img209.gif)
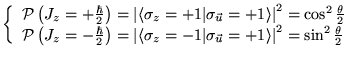
La somme des probabilités vaut bien ![]()
La valeur moyenne est :