
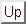


suivant: 1.8 Exemples physiques: le
monter: 1 Théorie générale des
précédent: 1.6 Spin
Table des matières
Sous-sections
Si les deux systèmes sont
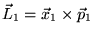 et
et
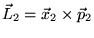 (moments cinétiques), on forme
alors
(moments cinétiques), on forme
alors
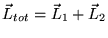 . Si
. Si
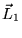 et
et
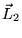 sont conservés (ex: forces centrales sur
sont conservés (ex: forces centrales sur 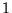 et
et 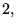
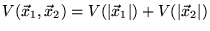 )
et donc
)
et donc
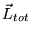 sera conservé (indépendant du temps). On peut fixer
simultanément
sera conservé (indépendant du temps). On peut fixer
simultanément
 et
et
 (
(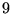 quantités).
quantités).
Si on a 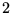 ensembles
ensembles
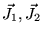 de type moment cinétique,
c'est-à-dire :
de type moment cinétique,
c'est-à-dire :
Si on introduit 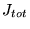 comme
comme
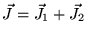 alors
alors
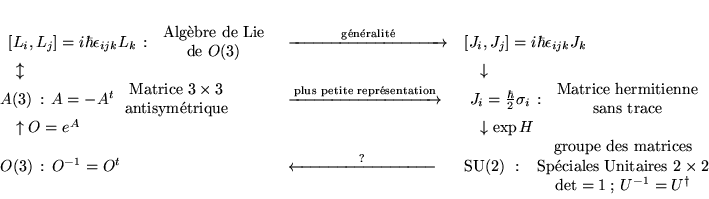
![$ [J_{i},J_{j}]=i\hbar \epsilon _{ijk}J_{k} $](img230.gif)
Example
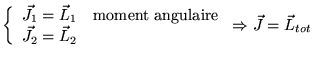
- Question
- En mécanique quantique, on a besoin d'ECOC. Quels ECOC peut-on trouver
? (quelles bases ?)
Example
Soient
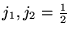
et
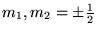
on est donc à
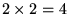
dimensions.
Or :
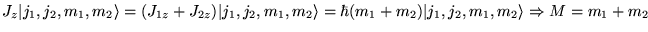
Il y 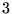 cas possibles :
cas possibles :
Soit
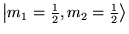 sur lequel
on applique
sur lequel
on applique
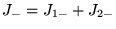 donc
donc
Car:
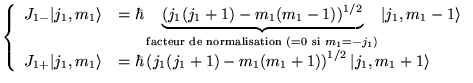
Finalement,
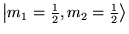 est l'état où
est l'état où
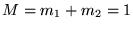 est maximal.
est maximal.
Conclusion
Il nous reste à normaliser l'équation suivante par
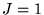
. Cette normalisation
va nous faire trouver le coefficient de Clebsch-Gordan.
Note
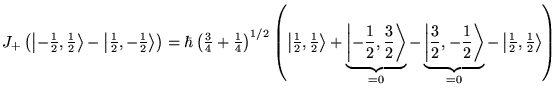
- En normalisant
-
On est toujours à dimension
 : on vient d'écrire
: on vient d'écrire 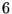 éléments, les
éléments, les 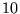 autres sont nuls.
autres sont nuls.
- Cas général
-
-
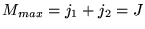 :
:
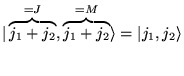
En agissant avec 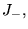 on a
on a
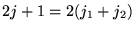 états
états
-
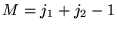 est
est  fois dégénéré .
fois dégénéré .
On a donc :
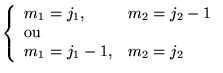
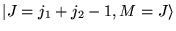 est orthogonal avec le vecteur où on fait
agir
est orthogonal avec le vecteur où on fait
agir 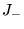 sur l'état maximal :
sur l'état maximal :
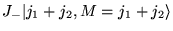
-
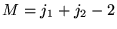 est
est 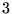 fois dégénéré.
fois dégénéré.
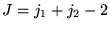 s'obtient en prenant un vecteur orthogonal
s'obtient en prenant un vecteur orthogonal
 et
et
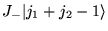
- Réponse
- La correspondance entre
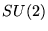 et
et 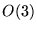 se fait par
se fait par
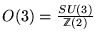 avec
avec
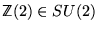
Example
La matrice suivante appartient au centre de
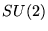
;
ie elle commute
avec toute
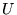
de
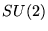
.
Donc on peut prendre :
Donc la correspondance ne se fait que dans un seul sens:
En divisant par
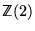 , on enlève le problème du spin
, on enlève le problème du spin 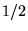 .
.
Note
À un élément de
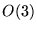
(c'est-à-dire
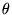
) correspond
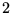
éléments de
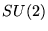
(c'est-à-dire
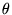
et
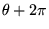
)

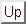


suivant: 1.8 Exemples physiques: le
monter: 1 Théorie générale des
précédent: 1.6 Spin
Table des matières
2000-10-19
![]() et
et
![]() (moments cinétiques), on forme
alors
(moments cinétiques), on forme
alors
![]() . Si
. Si
![]() et
et
![]() sont conservés (ex: forces centrales sur
sont conservés (ex: forces centrales sur ![]() et
et ![]()
![]() )
et donc
)
et donc
![]() sera conservé (indépendant du temps). On peut fixer
simultanément
sera conservé (indépendant du temps). On peut fixer
simultanément
![]() et
et
![]() (
(![]() quantités).
quantités).
![]() ensembles
ensembles
![]() de type moment cinétique,
c'est-à-dire :
de type moment cinétique,
c'est-à-dire :
![$\displaystyle \left\{ \begin{array}{l}
\left[ J_{1i},J_{1j}\right] =i\hbar \sum...
...hbar \sum _{i,j,k}J_{2k}\\
\left[ J_{1i},J_{2j}\right] =0
\end{array}\right. $](img227.gif)
![]() comme
comme
![]() alors
alors
![]()
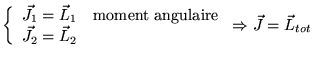
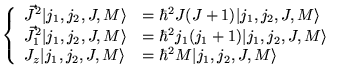
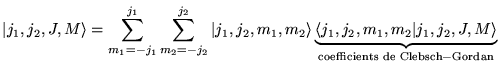
![]()
![]() cas possibles :
cas possibles :
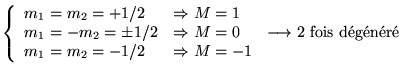
![]() sur lequel
on applique
sur lequel
on applique
![]() donc
donc
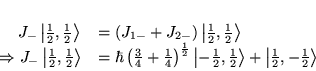
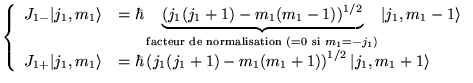
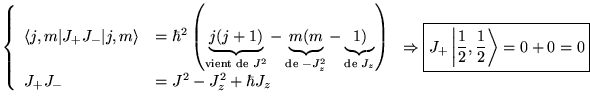
![]() est l'état où
est l'état où
![]() est maximal.
est maximal. 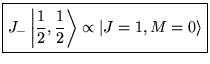
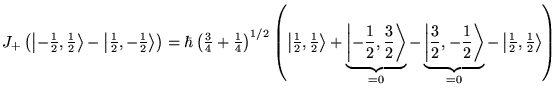
![]()
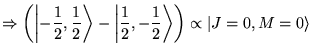
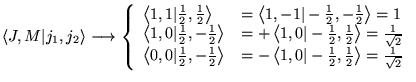
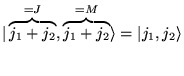
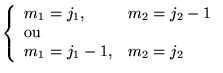
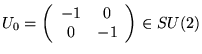
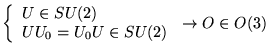
![]() , on enlève le problème du spin
, on enlève le problème du spin ![]() .
.