



suivant: 5.6 Points singuliers irréguliers
monter: 5 Equations Différentielles
précédent: 5.4 Équations linéaires d'ordre
Table des matières
Sous-sections
On peut trouver la SGEH par développement en série. On a de plus le théorème
de Fuchs pour la singularité des solutions de:
Note
Dans la suite, on fait les changements de notation suivants:
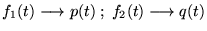
Définition
Si
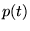
et
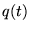
ont une singularité en un point
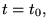
et si pour toute solution
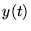
il existe
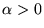
tel que
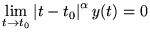
,
alors on dit que
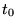
est point
singulier régulier de l'équation
différentielle.
Contre-exemple:
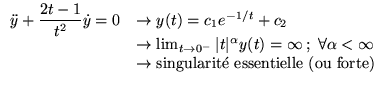
Remarque
Le développement de Taylor pour
existe, mais converge
vers la fonction nulle
Théorème
Un point singulier
est régulier ssi

Autour d'un point régulier, on peut écrire:
et chercher au moins une solution sous la forme:
dans laquelle 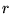 est solution de l'équation caractéristique (ou aux indices):
est solution de l'équation caractéristique (ou aux indices):
Preuve.
On utilise les expressions de
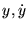
et
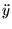
:
![$ \displaystyle \rightarrow L[y]=0=\sum ^{\infty }_{l=0}(t-t_{0})^{r+l-2}\left[ ...
..._{m=0}q_{m}a_{l-m}+\sum ^{l}_{m=0}p_{m}a_{l-m}(r+l-m)+a_{l}(r+l)(r+l-1)\right] $](img862.gif)
Ceci doit être vrai pour tout 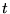 donc
donc
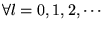 avec
avec
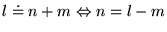
D'où:
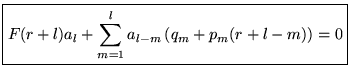
Il y a donc deux cas possibles:

- Si
 est un couple de solutions linéairement indépendantes
de
est un couple de solutions linéairement indépendantes
de
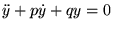
- Si
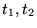 sont des zéros consécutifs de
sont des zéros consécutifs de 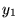
- Si
![$ y_{1},y_{2},p\in C^{0}_{[t_{1},t_{2}]} $](img886.gif) (régulières dans cet intervalle)
(régulières dans cet intervalle)
Alors
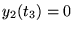 pour
pour
![$ t_{3}\in [t_{1},t_{2}] $](img888.gif)
 (une seule fois)
(une seule fois)
Exemple
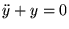
Il y en a  :
:
Autour de  pour solution
pour solution
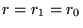 :
:
Termes d'ordre 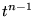 :
:
![% latex2html id marker 17324
$ \begin{array}{ll}
\Leftrightarrow a_{n}n(n+\gamma...
... )+\alpha \beta \right] \\
& =a_{n-1}[(n+\alpha -1)(n+\beta -1)]
\end{array} $](img902.gif)
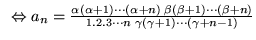
La série converge absolument si
On peut utiliser 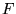 pour exprimer un grand nombre de fonctions:
pour exprimer un grand nombre de fonctions:
-
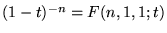
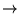 série géométrique, EDL satisfaite:
série géométrique, EDL satisfaite:
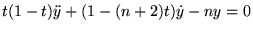
-
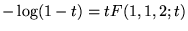 , EDL satisfaite:
, EDL satisfaite:
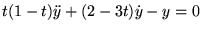
-
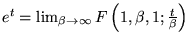
-
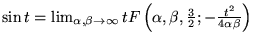
-
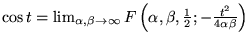
Les 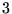 dernières fonctions font apparaître
dernières fonctions font apparaître
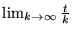 .
Ceci veut dire que le point singulier en
.
Ceci veut dire que le point singulier en
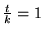 de
de 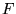 se
retrouve en
se
retrouve en
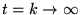 : confluence des
: confluence des 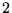 singularités
singularités 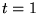 et
et 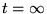 . Ceci est nécessaire pour avoir
la singularité essentielle de
. Ceci est nécessaire pour avoir
la singularité essentielle de
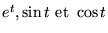 pour
pour
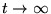 .
.




suivant: 5.6 Points singuliers irréguliers
monter: 5 Equations Différentielles
précédent: 5.4 Équations linéaires d'ordre
Table des matières
2000-10-06
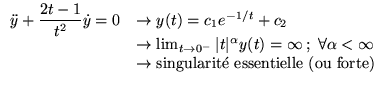

![]() ou
ou ![]() sont holomorphes en
sont holomorphes en ![]() alors
alors ![]() est
holomorphe.
est
holomorphe.![$\displaystyle \left\{ \begin{array}{l}
p(t)=\frac{1}{t-t_{0}}[p_{0}+p_{1}(t-t_{...
...-t_{0})+\cdots +q_{n}(t-t_{0})^{n}+\cdots ]}{(t-t_{0})^{2}}
\end{array}\right. $](img853.gif)
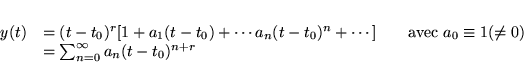
![]() est solution de l'équation caractéristique (ou aux indices):
est solution de l'équation caractéristique (ou aux indices):
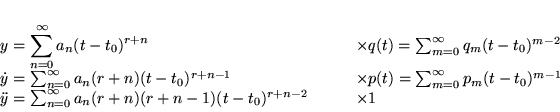
![$ \displaystyle \rightarrow L[y]=0=\sum ^{\infty }_{l=0}(t-t_{0})^{r+l-2}\left[ ...
..._{m=0}q_{m}a_{l-m}+\sum ^{l}_{m=0}p_{m}a_{l-m}(r+l-m)+a_{l}(r+l)(r+l-1)\right] $](img862.gif)
![]() donc
donc
![]() avec
avec
![]()
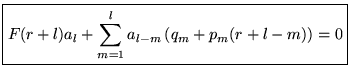
![]()
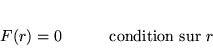
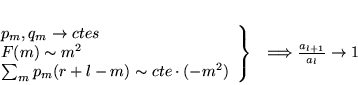
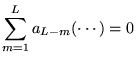 n'est pas nécessairement satisfaite!
n'est pas nécessairement satisfaite!
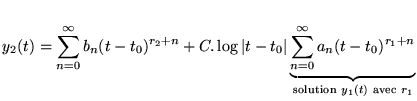
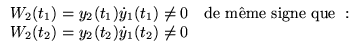
![]() change de signe puisque régulière donc
change de signe puisque régulière donc ![]() change
de signe
change
de signe
![]() Les zéros de
Les zéros de ![]() et
et ![]() sont entrelacés,
en dehors des points singuliers.
sont entrelacés,
en dehors des points singuliers.
![]()
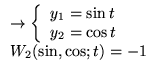
![]() :
:
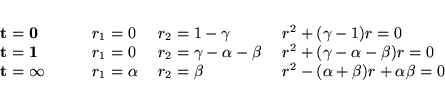
![]() pour solution
pour solution
![]() :
:
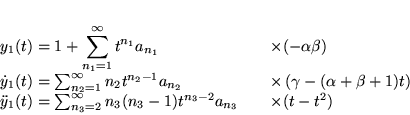
![]() :
:
![% latex2html id marker 17322
$\displaystyle \; \quad a_{n}\left[ \underbrace{n(n...
...ightarrow n-1}-\underbrace{\alpha \gamma }_{n_{1}\leftrightarrow n-1}\right] =0$](img901.gif)
![% latex2html id marker 17324
$ \begin{array}{ll}
\Leftrightarrow a_{n}n(n+\gamma...
... )+\alpha \beta \right] \\
& =a_{n-1}[(n+\alpha -1)(n+\beta -1)]
\end{array} $](img902.gif)
![]()

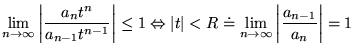
![]() pour exprimer un grand nombre de fonctions:
pour exprimer un grand nombre de fonctions: