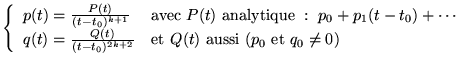
Point singulier régulier: rang ![]()
Point singulier irrégulier: rang ![]()
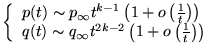 avec
avec
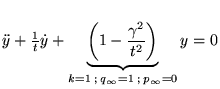
Lorsque
![]() :
:
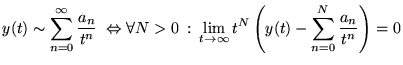
![]() La série partielle
La série partielle
![]() fournit une approximation de
fournit une approximation de ![]() d'autant meilleure que
d'autant meilleure que ![]() est
grand (l'erreur est en
est
grand (l'erreur est en
![]() )
)
Attention: Il n'y a pas nécessairement convergence: à ![]() fixé,
fixé,
![]() est éventuellement plus mauvais que
est éventuellement plus mauvais que ![]() . Donc
si on veut une meilleure précision, il faut prendre
. Donc
si on veut une meilleure précision, il faut prendre ![]() plus grand.
plus grand.
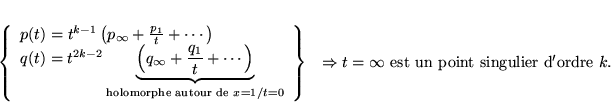
Si
![]() pour
pour
![]()
Alors on a des solutions sous forme de séries formelles:
![$\displaystyle y(t)\sim \exp \left[ \mu _{k}\frac{t^{k}}{k}+\mu _{k-1}t^{k-1}+\c...
...] \left( a_{\infty }+\frac{a_{1}}{t}+\cdots \frac{a_{n}}{t^{n}}+\cdots \right) $](img943.gif)
et chaque série formelle est le développement asymptotique d'une vraie solution:
![$\displaystyle \textrm{lorsque }t\rightarrow \infty \: :\: \frac{y(t)}{\exp \lef...
...u _{0}\ln t\right] }\sim a_{\infty }+\frac{a_{1}}{t}+\frac{a_{2}}{t^{2}}\cdots $](img944.gif)
![% latex2html id marker 17463
$ \begin{array}{lll}
\textrm{Si} & y(t) & =e^{f(t)}...
...n}+2\dot{f}\sum (-n)a_{n}t^{-n-1}+\sum n(n+1)a_{n}t^{-n-2}\right]
\end{array} $](img945.gif)
Comme
![]() et
et
![]() et
et
![]() , alors
, alors
![]() donne le comportement dominant à grand
donne le comportement dominant à grand ![]() .
.
En général, ![]() s'écrit (où un terme n'est sommé sur un indice que
si cet indice apparaît):
s'écrit (où un terme n'est sommé sur un indice que
si cet indice apparaît):
![\begin{displaymath}
% latex2html id marker 17477\begin{array}{ll}
\displaystyl...
...-1-n}\\
& \left. +q_{m}a_{n}t^{2k-2-n}\right] =0
\end{array}\end{displaymath}](img950.gif)
![% latex2html id marker 17479
$ \begin{array}{lll}
\ast \: t^{2k-2} & \rightarrow...
...}\left[ \mu _{k}^{2}+(2k-1)\mu _{2k}+p_{0}\mu _{k}+q_{0}\right] =0
\end{array} $](img951.gif)
![]()
![]()