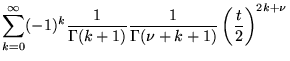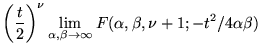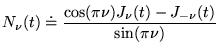suivant: 8.4 Équation et polynomes
monter: 8 Quelques fonctions spéciales
précédent: 8.2 Équation et fonction
Table des matières
Sous-sections
est une solution de
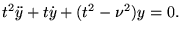 |
(8.3.3) |
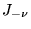 est aussi solution, puisque seul
est aussi solution, puisque seul 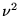 apparait
dans l'équation.
apparait
dans l'équation.
- Si
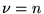 entier, en posant
entier, en posant 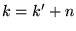 dans (8.3.1), on a
dans (8.3.1), on a
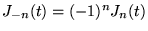 qui n'est donc pas linéairement independante
de
qui n'est donc pas linéairement independante
de 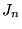 .
.
- L'autre solution est alors donnée par la fonction de Neumann:
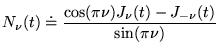 |
(8.3.4) |
qui reste finie pour
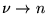 , contient un terme en
, contient un terme en 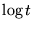 ,
et est indépendante grâce à la
,
et est indépendante grâce à la
- Formule de Lommel: (Wronskien des solutions
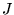 et
et 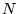 )
)
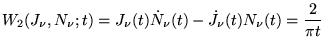 |
(8.3.5) |
-
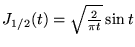 ;
;
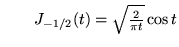 .
.
- Fonction génératrice: série de Fourier d'une onde plane
à 2 dimensions:
- Récurrences:
| |
|
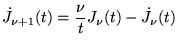 |
(8.3.8) |
| |
|
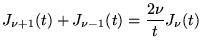 |
(8.3.9) |
- Série asymptotique:
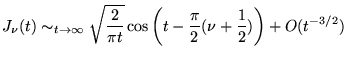 |
(8.3.10) |
- Orthogonalité: Si
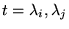 sont des
zéros différents
sont des
zéros différents
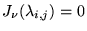 ,
,
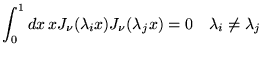 |
(8.3.11) |
- Zéros: Dans le plan complexe
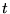 ,
, 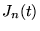 ne s'annule
que pour
ne s'annule
que pour 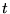 réel.
réel. 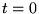 est un zéro d'ordre
est un zéro d'ordre 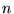 , les
zéros suivants
, les
zéros suivants
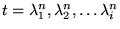 sont simples. Pour grand
sont simples. Pour grand 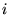 , on peut approcher le
, on peut approcher le 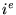 zéro
par la formule asymptotique
zéro
par la formule asymptotique
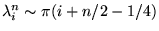 découlant
de (8.3.10). Pour avoir une idée de l'erreur, l'approximation asymptotique
est donnée entre parenthèses après chaque valeur exacte dans
le tableau suivant.
découlant
de (8.3.10). Pour avoir une idée de l'erreur, l'approximation asymptotique
est donnée entre parenthèses après chaque valeur exacte dans
le tableau suivant.
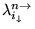 |
0 |
1 |
2 |
3 |
| 1 |
2.40 (2.36) |
3.83 (3.93) |
5.14 (5.5) |
6.38 (7.07) |
| 2 |
5.52 (5.50) |
7.02 (7.07) |
8.42 (8.64) |
9.76 (10.21) |
| 3 |
8.65 (8.64) |
10.17 (10.21) |
11.62 (11.78) |
13.02 (13.35) |
| 4 |
11.79 (11.78) |
|
|
|
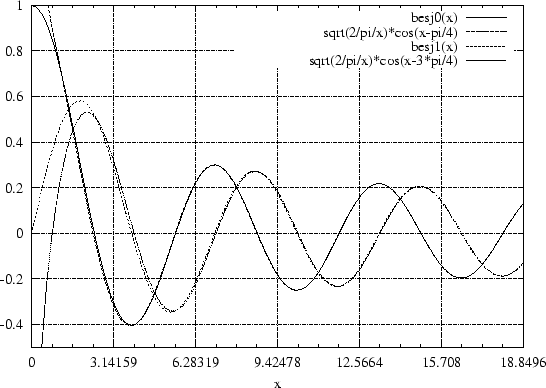
Figure 8.3.1:
Les fonctions de Bessel
 et
et
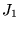 et leurs approximations asymptotiques (8.3.10).
et leurs approximations asymptotiques (8.3.10).
|
|
- Application: D'après (8.3.6),
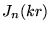 est une
superposition d'ondes planes
est une
superposition d'ondes planes
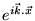 à 2 dimensions,
dont le module
à 2 dimensions,
dont le module 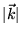 est fixé. C'est donc une fonction propre
du Laplacien
est fixé. C'est donc une fonction propre
du Laplacien
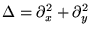 avec la valeur
propre
avec la valeur
propre
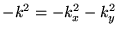 . Les modes propres
. Les modes propres 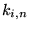 d'un tambour de rayon
d'un tambour de rayon 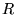 s'obtiennent en demandant que
s'obtiennent en demandant que
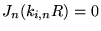 (la membrane est fixée au bord), et sont donc déterminés par
les zéros
(la membrane est fixée au bord), et sont donc déterminés par
les zéros
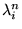 des fonctions de Bessel.8.3 On rencontre aussi les fonctions de Bessel dans tous les problèmes à
symétrie cylindrique (cables coaxiaux, etc.).
des fonctions de Bessel.8.3 On rencontre aussi les fonctions de Bessel dans tous les problèmes à
symétrie cylindrique (cables coaxiaux, etc.).




suivant: 8.4 Équation et polynomes
monter: 8 Quelques fonctions spéciales
précédent: 8.2 Équation et fonction
Table des matières
2000-10-06