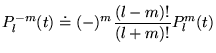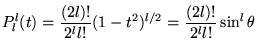suivant: 8.5 Harmoniques sphériques
monter: 8 Quelques fonctions spéciales
précédent: 8.3 Équation et fonction
Table des matières
Sous-sections
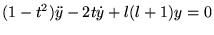 |
(8.4.1) |
C'est un cas particulier de l'équation hypergéométrique, avec
les substitutions:
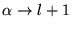 (entier),
(entier),
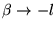 ,
,
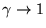 ,
,
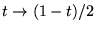 . Une des 2 solutions
est un Polynome de Legendre:
. Une des 2 solutions
est un Polynome de Legendre:
L'autre solution 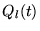 a une singularité logarithmique en
a une singularité logarithmique en 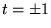 .
.
-
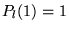
- Premiers polynomes: (
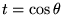 )
)
- Fonction génératrice:
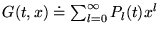 .
En utilisant des variables plus parlantes
.
En utilisant des variables plus parlantes
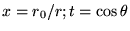 , on
a:
, on
a:
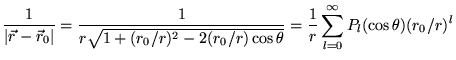 |
(8.4.4) |
- Application: un
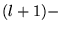 pôle linéaire est un ensemble
de
pôle linéaire est un ensemble
de 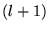 charges de valeurs
charges de valeurs
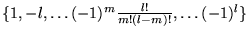 ,
situées sur l'axe
,
situées sur l'axe 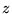 où elles sont également espacées
d'une distance
où elles sont également espacées
d'une distance 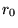 . Un tel
. Un tel 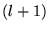 -pôle peut être obtenu
par récurrence en prenant 2
-pôle peut être obtenu
par récurrence en prenant 2 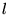 -pôles de charges opposées,
et en les décalant de la distance
-pôles de charges opposées,
et en les décalant de la distance 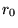 . À des distances
. À des distances 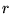 grandes devant
grandes devant 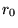 , le potentiel électrostatique d'un
, le potentiel électrostatique d'un 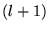 -pôle
est :
-pôle
est :
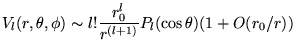 |
(8.4.5) |
Les polynômes de Legendre donnent donc la dépendance angulaire à
grande distance de ces 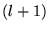 -pôles linéaires. Pour
-pôles linéaires. Pour 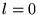 ,
on a un monopole électrique et donc une charge usuelle: le potentiel
,
on a un monopole électrique et donc une charge usuelle: le potentiel
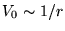 est à symétrie sphérique indépendant de
est à symétrie sphérique indépendant de 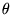 .
Pour
.
Pour 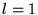 , on a un dipôle usuel, avec
, on a un dipôle usuel, avec
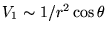 .
Le nombre
.
Le nombre 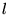 est le nombre de fois où le potentiel s'annule quand on passe
(le long d'un cercle) de l'axe
est le nombre de fois où le potentiel s'annule quand on passe
(le long d'un cercle) de l'axe 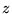 positif (
positif (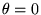 ) à l'axe négatif
(
) à l'axe négatif
(
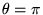 ).
).
- Récurrences:
- Équation de Legendre sous forme d'équation aux valeurs propres d'un
opérateur différentiel symétrique:
![$\displaystyle L[y]=\lambda y;\qquad L[y]=\frac{d}{dt}\left[ (1-t^{2})\frac{d}{dt}y\right] ;\qquad \lambda =-l(l+1).$](img1327.gif) |
(8.4.7) |
- Orthogonalité:
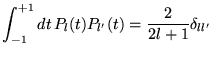 |
(8.4.8) |
- Définition:
![$\displaystyle P_{l}^{m}(t)\doteq (1-t^{2})^{m/2}\frac{d^{m}}{dt^{m}}P_{l}(t)=\frac{1}{2^{l}l!}\left[ \frac{d}{dt}\right] ^{l+m}(t^{2}-1)^{l}$](img1329.gif) |
(8.4.9) |
est solution de8.4
![$\displaystyle \frac{d}{dt}\left[ (1-t^{2})\frac{d}{dt}y\right] +\left[ l(l+1)-\frac{m^{2}}{1-t^{2}}\right] y=0.$](img1331.gif) |
(8.4.10) |
- Extension: pour
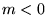 , on définit
, on définit
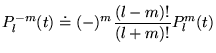 |
(8.4.11) |
- Valeurs particulières:
- Récurrences:
- Orthonormalisation:
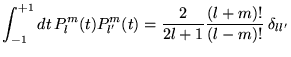 |
(8.4.14) |




suivant: 8.5 Harmoniques sphériques
monter: 8 Quelques fonctions spéciales
précédent: 8.3 Équation et fonction
Table des matières
2000-10-06
![]() a une singularité logarithmique en
a une singularité logarithmique en ![]() .
.
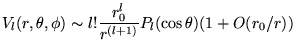
![$\displaystyle L[y]=\lambda y;\qquad L[y]=\frac{d}{dt}\left[ (1-t^{2})\frac{d}{dt}y\right] ;\qquad \lambda =-l(l+1).$](img1327.gif)