



suivant: 8.6 Autres polynômes orthogonaux
monter: 8 Quelques fonctions spéciales
précédent: 8.4 Équation et polynomes
Table des matières
Sous-sections
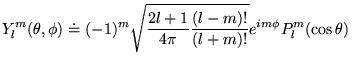 |
(8.5.1) |
- Le laplacien en coordonnées sphériques peut s'écrire
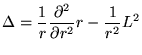 |
(8.5.2) |
où on sépare l'opérateur différentiel angulaire:
![% latex2html id marker 18745
$\displaystyle -L^{2}=\left[ \frac{\partial^{2}}{\p...
...eta }+\frac{1}{\sin ^{2}\theta }\frac{\partial^{2}}{\partial\phi ^{2}}\right] .$](img1345.gif) |
(8.5.3) |
Pour trouver des fonctions  harmoniques (i.e, solutions de
harmoniques (i.e, solutions de
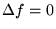 ), sous forme séparée
), sous forme séparée
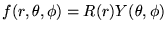 sphérique, il suffit de résoudre une équation différentielle
sphérique, il suffit de résoudre une équation différentielle
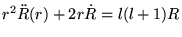 pour trouver
pour trouver 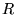 chaque fois
que l'on connait une fonction propre de
chaque fois
que l'on connait une fonction propre de
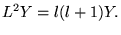 |
(8.5.4) |
Puisque 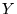 doit être périodique en
doit être périodique en 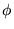 , on l'écrit
comme une série de Fourier:
, on l'écrit
comme une série de Fourier:
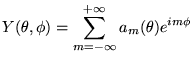 |
(8.5.5) |
et l'équation aux valeurs propres
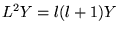 devient une équation
différentielle pour les coefficients
devient une équation
différentielle pour les coefficients 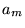 :
:
que nous reconnaissons comme l'équation pour les fonctions de Legendre
associées (8.4.10). On a donc à un facteur de normalisation
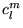 près,
près,
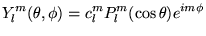 |
(8.5.8) |
- Orthonormalisation: les
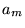 sont donc proportionnelles aux
fonctions de Legendre associées, et convient de les normaliser à:
sont donc proportionnelles aux
fonctions de Legendre associées, et convient de les normaliser à:
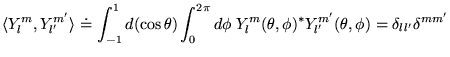 |
(8.5.9) |
- Complétude: Toute fonction continue sur la sphère unité
peut se développer sur la base des
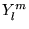 :
:
- Premières harmoniques sphériques:
- Effet des rotations: sous une rotation à 3 dimensions
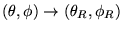 ,
,
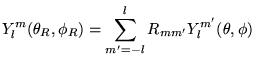 |
(8.5.12) |
où 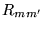 est une certaine matrice
est une certaine matrice
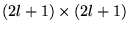 ,
dépendant de la rotation choisie, et qui la représente dans l'espace
des fonctions à
,
dépendant de la rotation choisie, et qui la représente dans l'espace
des fonctions à 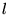 fixé. Cette matrice est unitaire car la relation
d'orthonormalisation (8.5.9) est invariante.
fixé. Cette matrice est unitaire car la relation
d'orthonormalisation (8.5.9) est invariante.
- Théorème d'addition:
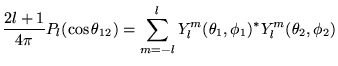 |
(8.5.13) |
si
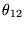 est l'angle entre les vecteurs
est l'angle entre les vecteurs
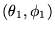 et
et
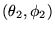 .8.5
.8.5




suivant: 8.6 Autres polynômes orthogonaux
monter: 8 Quelques fonctions spéciales
précédent: 8.4 Équation et polynomes
Table des matières
2000-10-06
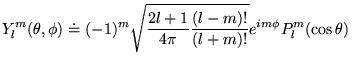
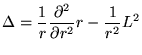
![% latex2html id marker 18745
$\displaystyle -L^{2}=\left[ \frac{\partial^{2}}{\p...
...eta }+\frac{1}{\sin ^{2}\theta }\frac{\partial^{2}}{\partial\phi ^{2}}\right] .$](img1345.gif)
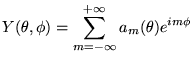
![% latex2html id marker 18776
$\displaystyle -\frac{d^{2}}{d\theta ^{2}}a_{m}(\th...
...}{d\theta }a_{m}(\theta )=[l(l+1)-\frac{m^{2}}{\sin ^{2}\theta }]a_{m}(\theta )$](img1353.gif)
![% latex2html id marker 18782
$\displaystyle -(1-t^{2})\ddot{a}_{m}(t)+2t\dot{a}_{m}(t)=[l(l+1)-\frac{m^{2}}{1-t^{2}}]a_{m}(t);\qquad t=\cos \theta$](img1354.gif)