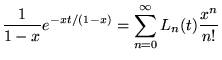


suivant: À propos de ce
monter: 8 Quelques fonctions spéciales
précédent: 8.5 Harmoniques sphériques
Table des matières
Sous-sections
L'équation aux valeurs propres
![$\displaystyle L[y_{n}]=\alpha (t)\ddot{y}_{n}+\beta (t)\dot{y}_{n}=\lambda _{n}y_{n}$](img1383.gif) |
(8.6.1) |
aura une solution polynomiale
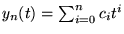 avec,
pour chaque
avec,
pour chaque 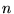 , une valeur propre appropriée
, une valeur propre appropriée
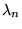 si et seulement si:8.6
si et seulement si:8.6
 |
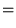 |
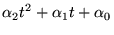 |
(8.6.2) |
 |
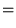 |
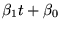 |
(8.6.3) |
 |
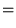 |
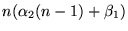 |
(8.6.4) |
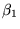 |
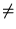 |
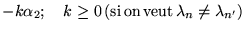 |
(8.6.5) |
L'équation (8.6.1) est donc de type hypergéométrique
de Gauss.
L'opérateur 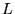 n'est pas symétrique par rapport au produit scalaire
usuel, mais en le multipliant par une fonction
n'est pas symétrique par rapport au produit scalaire
usuel, mais en le multipliant par une fonction 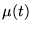 telle que
telle que
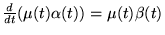 ,
on obtient un opérateur symétrique8.7
,
on obtient un opérateur symétrique8.7
pour toutes fonctions  annulant le dernier terme aux limites. Si
ces fonctions sont polynomiales, leur Wronskien aussi, et pour annuler le terme
aux limites, il suffit donc de demander:
annulant le dernier terme aux limites. Si
ces fonctions sont polynomiales, leur Wronskien aussi, et pour annuler le terme
aux limites, il suffit donc de demander:
pour n'importe quelle puissance  . Alors, puisque
. Alors, puisque
![$ \langle z,L_{s}[y]\rangle =\langle z,L[y]\rangle _{\mu } $](img1407.gif) ,
on a l'orthogonalité des solutions
,
on a l'orthogonalité des solutions  par rapport à la mesure
par rapport à la mesure
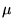 :
:
| |
|
![$\displaystyle \langle y_{n},L[y_{n'}]\rangle _{\mu }-\langle L[y_{n}],y_{n'}\rangle _{\mu }=(\lambda _{n'}-\lambda _{n})\langle y_{n},y_{n'}\rangle _{\mu }$](img1409.gif) |
(8.6.11) |
| |
|
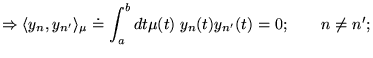 |
(8.6.12) |
| |
|
![% latex2html id marker 19015
$\displaystyle \langle y_{n},L[y_{n}]\rangle _{\mu ...
...y_{n},y_{n}\rangle _{\mu }=-\int _{a}^{b}dt\, \mu (t)\alpha (t)\dot{y}_{n}^{2}.$](img1411.gif) |
(8.6.13) |
Puisque 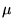 est défini positif, les
est défini positif, les
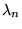 sont donc
de signe opposé à
sont donc
de signe opposé à 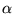 (dont les zéros sont des points
singuliers de 8.6.1).
(dont les zéros sont des points
singuliers de 8.6.1).
![$\displaystyle \Pi _{n}(t)=\frac{1}{\mu (t)}\frac{d^{n}}{dt^{n}}[\mu (t)\alpha (t)^{n}]$](img1412.gif) |
(8.6.14) |
est un polynôme solution de (8.6.1). Démonstration:
-
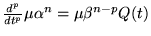 , où
, où 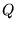 est un polynome de degré
est un polynome de degré 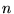 . En effet, si
. En effet, si 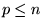 , il y a
toujours assez de puissances de
, il y a
toujours assez de puissances de 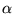 pour utiliser
pour utiliser
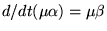 .
Comme
.
Comme 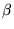 est un polynôme (de degré 1), on peut itérativement
construire le polynôme
est un polynôme (de degré 1), on peut itérativement
construire le polynôme 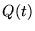 .
.
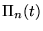 est donc bien un
polynôme de degré
est donc bien un
polynôme de degré 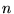 , que l'on peut développer sur la base
des
, que l'on peut développer sur la base
des 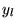 (solutions de 8.6.1 pour la valeur propre
(solutions de 8.6.1 pour la valeur propre
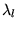 )
qui sont orthogonales et donc linéairement indépendantes:
)
qui sont orthogonales et donc linéairement indépendantes:
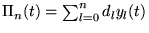 .
.
-
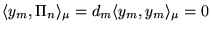 pour
pour  . En effet, intégrant
. En effet, intégrant
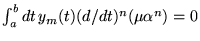
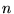 fois par parties, on arrive à
fois par parties, on arrive à
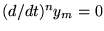 , et les
termes aux bords
, et les
termes aux bords
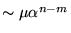 s'annulent grâce à
(8.6.9). Si
s'annulent grâce à
(8.6.9). Si 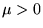 ,
,
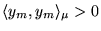 et on en déduit
et on en déduit 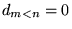 .
.
-
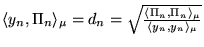 donne la normalisation.
donne la normalisation.
| |
|
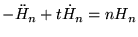 |
(8.6.15) |
| |
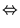 |
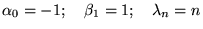 |
(8.6.16) |
| |
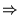 |
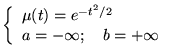 |
(8.6.17) |
Normalisation: la formule de Rodrigues donne:
| |
|
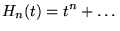 |
(8.6.18) |
| |
|
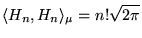 |
(8.6.19) |
Fonction génératrice:
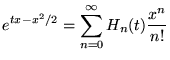 |
(8.6.20) |
Les polynômes d'Hermite donnent en mécanique quantique les fonctions
d'onde de l'oscillateur harmonique.
| |
|
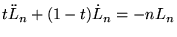 |
(8.6.21) |
| |
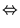 |
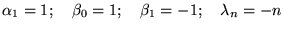 |
(8.6.22) |
| |
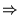 |
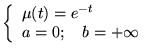 |
(8.6.23) |
Récurrence:
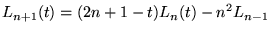 |
(8.6.24) |
Normalisation:
| |
|
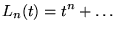 |
(8.6.25) |
| |
|
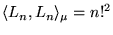 |
(8.6.26) |
Fonction génératrice:
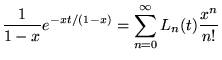 |
(8.6.27) |
Les polynômes de Laguerre donnent en mécanique quantique la dépendance
radiale des fonctions d'onde de l'atome d'hydrogène.
| |
|
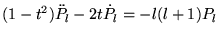 |
(8.6.28) |
| |
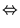 |
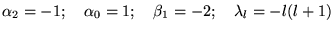 |
(8.6.29) |
| |
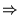 |
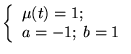 |
(8.6.30) |
Les polynômes de Legendre sont historiquement définis avec un facteur
par rapport à la formule de Rodrigues, cf 8.4.3. Ils interviennent
dans tous les problèmes à symétrie sphérique.
| |
|
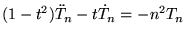 |
(8.6.31) |
| |
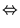 |
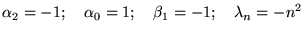 |
(8.6.32) |
| |
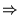 |
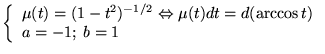 |
(8.6.33) |
En termes de la variable
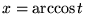 , l'équation devient
, l'équation devient
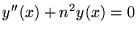 .
Les polynômes de Tchebycheff sont donc une façon d'exprimer
.
Les polynômes de Tchebycheff sont donc une façon d'exprimer 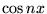 comme un polynôme en
comme un polynôme en 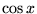 . Ils sont utiles pour dans les problèmes
d'interpolation.
. Ils sont utiles pour dans les problèmes
d'interpolation.



suivant: À propos de ce
monter: 8 Quelques fonctions spéciales
précédent: 8.5 Harmoniques sphériques
Table des matières
2000-10-06
![]() n'est pas symétrique par rapport au produit scalaire
usuel, mais en le multipliant par une fonction
n'est pas symétrique par rapport au produit scalaire
usuel, mais en le multipliant par une fonction ![]() telle que
telle que
![]() ,
on obtient un opérateur symétrique8.7
,
on obtient un opérateur symétrique8.7
![$\displaystyle L_{s}[y]=\mu (t)L[y]=\frac{d}{dt}\left[ \mu \alpha \frac{d}{dt}y\right]$](img1401.gif)
![% latex2html id marker 18979
$\displaystyle \langle z,L_{s}[y]\rangle =\int _{a}...
...t\, y(t)L_{s}[z]+\int _{a}^{b}dt\, \frac{d}{dt}[\mu \alpha (z\dot{y}-y\dot{z})]$](img1402.gif)
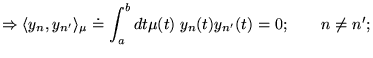
![% latex2html id marker 19015
$\displaystyle \langle y_{n},L[y_{n}]\rangle _{\mu ...
...y_{n},y_{n}\rangle _{\mu }=-\int _{a}^{b}dt\, \mu (t)\alpha (t)\dot{y}_{n}^{2}.$](img1411.gif)